Feedback Loop and ML
This page talks about how the ML pipeline when deployed in society can lead to a feedback loop.
-
Though as we will see later in these notes, the effect of the ML pipeline can change the history for the future.
Under Construction
This page is still under construction. In particular, nothing here is final while this sign still remains here.
A Request
I know I am biased in favor of references that appear in the computer science literature. If you think I am missing a relevant reference (outside or even within CS), please email it to me.
An overview
Recall that we have considered various notions of bias that can creep in when the ML pipeline interacts with society:
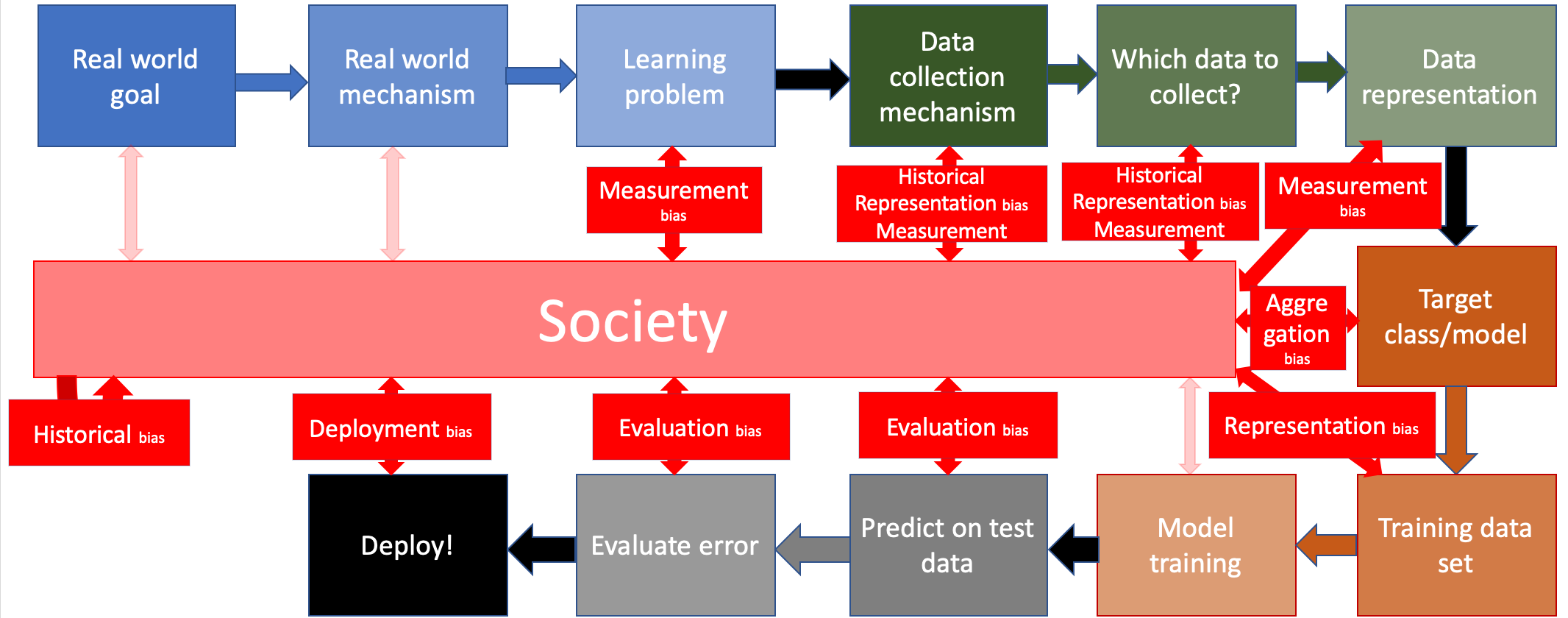
For simplicity assume that you as the ML pipeline designer has been able to get rid of all biases expect historical bias (because well, it is present in society to begin with and hence out of your control1) and measurement bias (because at some point, one will have to measure a proxy variable for the actual variable that might not be directly measurable). In other words, the situation looks like this:
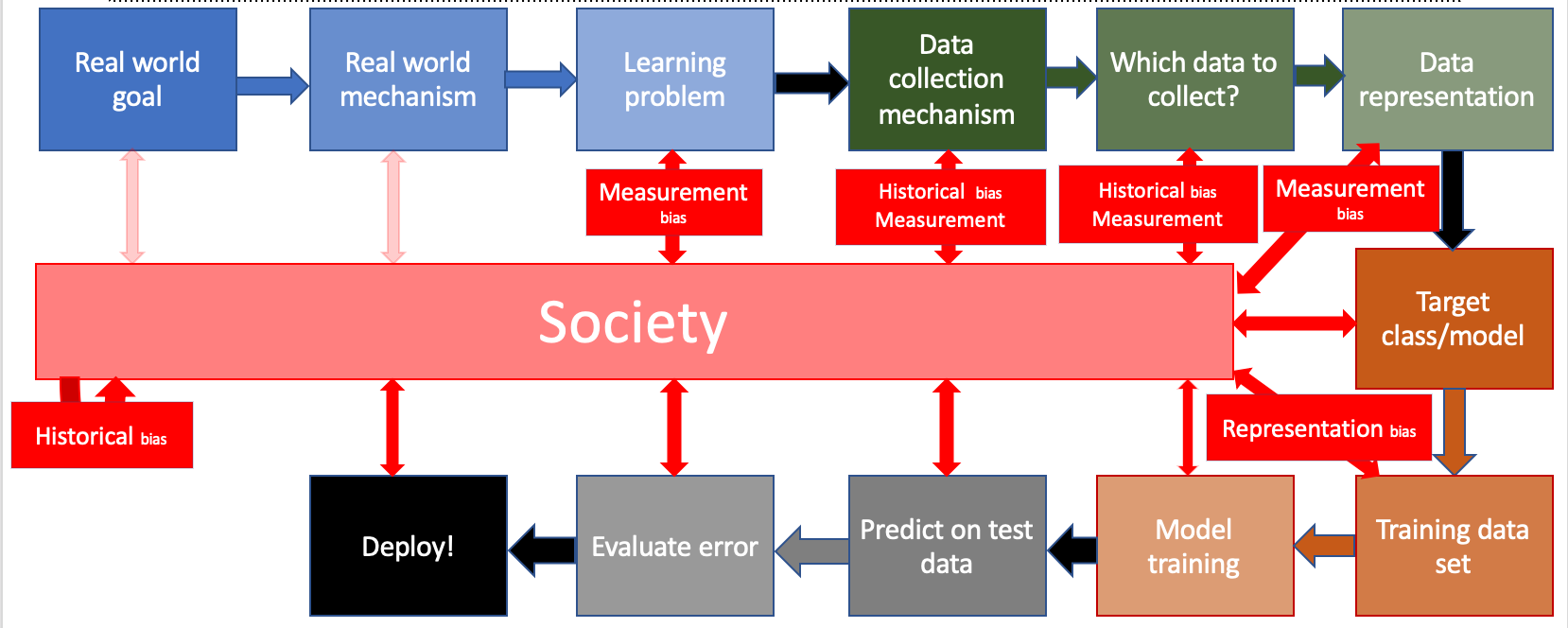
Now consider what happens when you deploy your ML pipeline in society and the deployment itself changes society in some way (and hence affects the next round of training of your model-- assuming you re-train your model to reflect changes in society, which most ML pipelines will do), like so (gif generated via ezgif ):
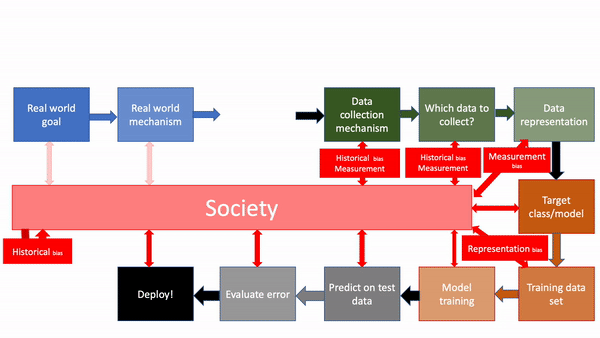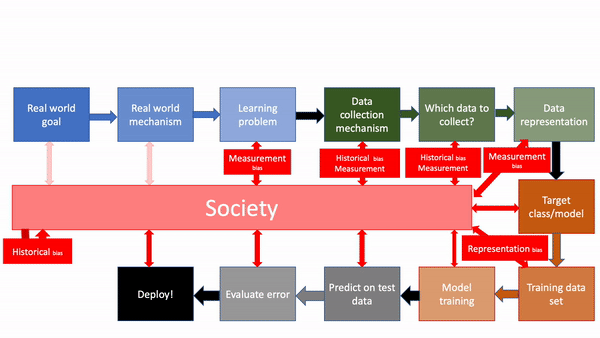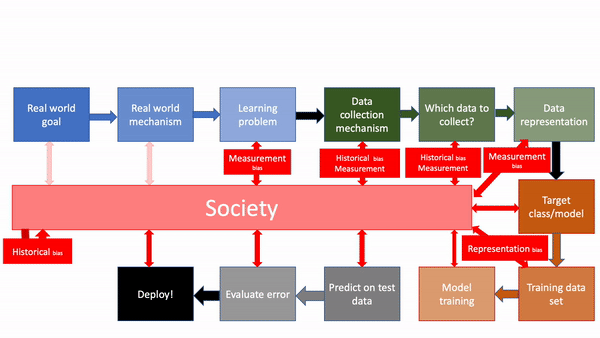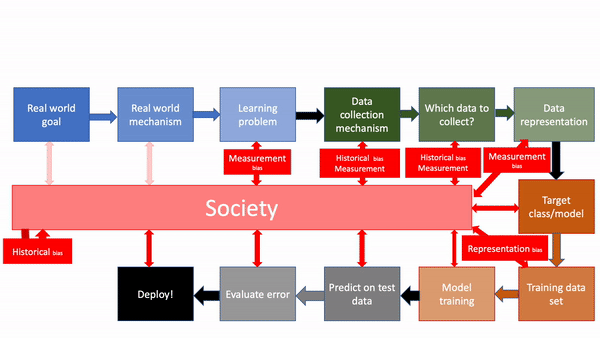
In other words, a model is developed that has some of the biases from society, which is then deployed back into society, where it changes the society (in particular, it can now contribute to historical and measurement bias in the future), which in turn changes the ML model for the future and the feedback loop continues:
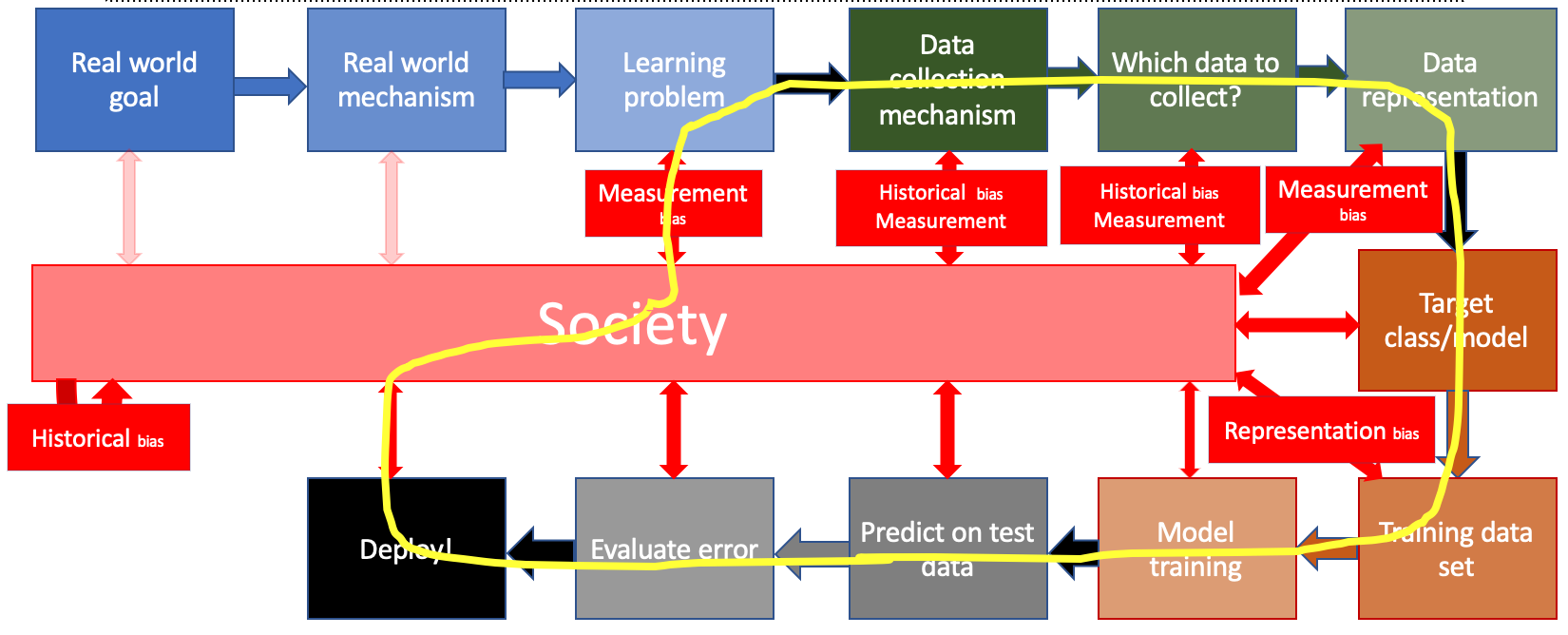
Predictive Policing
We will use predictive policing as the "application area" to talk about feedback loops. In short, predictive policing is the use of an ML pipeline to predict when and where crime is going to happen next. Such a tool is used by police departments to figure out "crime hot spots" so that it can send more cops to areas with higher risk of crime happening--
Of course by now y'all should realize that this can potentially be problematic:
What we will see in these notes is that using predictive policing along with the feedback loop mechanism can actually make things worse:
Exercise
Figure out how predictive policing can lead to a feedback loop.
Formalizing the intuition on feedback loops
So far we have seen intuitively that predictive policing can contribute to feedback loops, which can be harmful. But we need to go beyond intuition-- can we "prove" that predictive policing can lead to harmful feedback loops. We will see two ways of doing this-- one via simulations and another via theoretical modeling, which we do next.
Simulations for feedback loops
Acknowledgments
The setup and arguments in this section are heavily based on a Significance 2016 paper by Lum and Isaac.
Our goal in this section is to run simulations to show that using PredPol (or similar predictive policing algorithms) can lead to feedback loops. We will walk through the process of "re-creating" the set of Lum and Isaac. We start off with the high-level question:
How does one "show" a feedback loop?
There could be multiple ways to answer the question above. To direct our discussion somewhat, we will follow this high-level strategy: pick a certain city, say Buffalo:
For context, Lum and Isaac picked Oakland, CA:
The main idea is to run PredPol on historical crime data and observe whether it creates s feedback loop or not. Following Lum and Isaac, we will focus on drug arrests.
Why drug crime arrests?
At this point in the notes, it probably is obvious why drug arrest crimes were chosen. Yes, disproportionately more black Americans are arrested for drug crimes (even though drug usage does not have similar skew):
As we will see later in the notes, any imbalance in arrest rates across groups will most probably lead to a further imbalance in arrest rates once predictive policing is put in the mix. In other words, drug crime arrests seem to be a good application area where one could hope to show feedback loops if predictive policing is used.
For the rest of the section let us assume you have access to drug crimes arrests for say the year 2019 in Buffalo. This is a realistic assumption since many cities in the US male crime incidents data public: e.g. here are crime incidents reported in Buffalo .
What about access to PredPol?
We will assume that you have access to the PredPol algorithm. It turns out that there is enough information about the algorithm (see e.g. overview from PredPol that this is not an unreasonable assumption.
One of the videos above briefly talked about how PredPol works but here is a quick summary:
- The geographical areas are divided into "grids" and all the crime information is aggregated in each cell.
- PredPol (as per its founders and via Lum and Isaac) "only three data points in making predictions: past type of crime, place of crime and time of crime. It uses no personal information about individuals or groups of individuals, eliminating any personal liberties and profiling concerns."
The question(s) we want to answer
As one might imagine even though we made two assumptions above (i.e. we have access to drug crime data in Buffalo in 2019 and we have access to PredPol), there are still many more things that we will need to figure. To direct the discussion, let us state the two main questions we want to answer. The question is to do with the initial state: i.e. what happens if one uses PredPol only once and the feedback loop state, we consider the case that the police acts on PredPol's suggestion and the resulting drug crime arrest data is fed back into PredPol and the cycle continues.
Initial State Question
Here the question basically is the following. If we were to use PredPol to say decide on where potential drug crimes were to happen on January 1, 2019 in Buffalo, then how does PredPol's prediction compare to "actual" drug crimes on the same day.
Note The use of quotes in "actual" is on purpose-- we will come to this shortly.
Feedback Loop State Question
Here the question is actually to test whether predictive policing could lead to feedback loop. The idea is to simulate the use of PredPol in Buffalo from January 1, 2019 to December 31, 2019 in Buffalo and use the observed drug crime data for a given day to generate PredPol's prediction for the next day. The goal here is to check if the the odds of location being "targeted" by PredPol goes up (say when compared to the reported 2019 drug crimes as a baseline).
Initial state question
We will now focus on the initial state question. The big stumbling block is figuring out the actual number of occurrences of drug crimes in each grid cell in Buffalo. Here is one thing to try:
Exercise (using crime reports data)
You already have access to reported drug crimes data (which will also be used by PredPol): one option would be to use this option as a proxy for the actual occurrences of drug crimes. Is this fine? If so, why would this not be biased? If not, why not?
As we have seen in a video earlier, there is representation bias and measurement bias in police drug crime/arrest records, so if we use the reported crime data then we will not be getting close to the ground truth.
Hence we must use some other way to get our hand on the actual drug crime use. Of course, this is essentially impossible to do: how do you figure out the incidents of drug crime incidents in the past? You cannot go knock on doors and ask if the residents committed some drug crime on all the days in 2019? As an exercise figure out why this is not feasible!
As an aside (NSDUH)
As an important aside, while it is not possible to get data on drug usage on a say per-house basis, there do exist high quality surveys that collect information at a less granular level. Perhaps the most relevant survey is the National Survey on Drug Use and Health (NSDUH) :
With the aside out of the way, we now move on to actually figuring out the ground truth-- or more accurately a good approximation of the ground truth
Exercise (ground truth on actual drug use)
Figure out a mechanism by which to compute a reasonably accurate count of drug use in various grids in Buffalo.
Hint Think of how to use an ML pipeline to predict drug usage based on the information above on NSDUH.
Click here for the procedure used by Lum and Isaac
Here is a high-level summary of what Lum and Isaac did:
- They first created a synthetic population. In other words, there created a dataset of individuals in Oakland such that the dataset is demographically accurate. Specifically, they represented each individual by their sex, household income, age, race, and the geo‐coordinates of their home. These values were assigned so that the demographic aggregates of each component matched US census data to the most granular level possible.
- They used the NSDUH survey, which has information on the responder's demographic characteristics (i.e. sex, household income, age, and race) as well as their (reported) drug usage.
- They fit a model to predict an individual drug usage based on an individual demographic characteristics. In other words, they used the NSDUH as their training data set.
- They then used their model to predict drug usage on their synthetic dataset and add up the number of drug usage (i.e. number of drug crimes) in each cell of the grid.
Now with the most thorny question out of the way, let us go back to solving the initial state question:
Exercise (initial state question)
Now that you have solved the issue of figuring out the ground truth, go ahead and solve the initial state question.
At this point we have all the information to answer the initial state question. In particular, we have the ground truth about drug crimes as well the police data on reported drug crimes on each grid cell. Since we also assumed we had access to PredPol algorithm, we can run it on the reported drug crime data and see which grid cells PredPol predicts will be high crimes areas. Then it is just a matter of comparing the results.
Lum and Isaac found that for their simulation for Oakland, the police drug crimes reports were concentrated on two areas that are prominently non-white and poorer neighborhoods while the drug usage from their ground truth was even distributed over the city. In their simulations, not surprisingly, mimicked what the police drug crime data said-- i.e. it focused on the two neighborhoods with more reported drug crimes. When broken down by the race (in their synthetic population), blacks were twice as likely to be flagged than whites even though drug usage in their ground truth was roughly equal across racial groups. See the Lum and Isaac paper for a graphical display of these findings.
Feedback loop state question
We will now focus on the feedback loop state question. We begin with the following exercise:
Exercise (using PredPol only on historical data)
Consider the following simulation. From January 1, 2019 to December 31, 2019, we use the original drug crime data for a given day to generate PredPol's prediction for the next day.
Do you expect the above simulation result to show that the odds of location being "targeted" by PredPol go up (when compared to the reported 2019 drug crimes)? If so, why? If not, why not?
Since the effect of PredPol prediction is not fed back into PredPol, we should expect the odds of PredPol targeting an area to track the historical reported drug crimes.
We are ready to try and answer the question:
Exercise (feedback loop state question)
How would you go about incorporating the effect of PredPol's predictions into reported drug crimes? I.e. how would you incorporate the "feedback"?
Click here for how Lum and Isaac answered this question
One simple way to do this to increase the number of crimes reported in areas that PredPol recommend that police be sent. E.g., one could bump up the reported drug crimes in a area by $x\%$ (for some value of $x$) in all areas were police were sent by PredPol. In areas not targeted by PredPol, use the historical reported drug crime data. The idea here is that if more police are sent to an area then more crimes will be reported/arrests will be made. This updated crimes data is then fed into PredPol for get predictions for next day.
Lum and Isaac picked $x=20$ (i.e. they assumed that the areas where police were sent by PredPol will have $20\%$ reported crimes than the historical data. They were able to show a very definite uptick in PredPol continuing to send more police to some targeted areas. See the Lum and Isaac paper for a graphical display of these findings.
Lum and Isaac present a fairly compelling case for feedback loop via their simulation results but we will still try and poke holes into their approach (especially since one of them leads to the next section!):
Exercise (potential issues with the Lum and Isaac result)
Can you think of some weakness(es) in the Lum and Isaac result. In particular, if you were tasked with the job of poking holes in their setup how would you go about it? For example, can you think of ways that their conclusion might not be general enough?
Click here for one potential drawback
One potential issue is that the results are based on a synthetic population (as well as synthetic ground truth). While it is apparent that at the aggregate level, their population and ground truth are accurate (since they are based on solid surveys), one could argue that perhaps the feedback look observed is due to the specific synthetic population that was chosen. I.e. there could have been some weird co-incidence in the constructed synthetic population that led to the occurrence of the feedback loop then it being some general phenomenon.
We would hasten to state that the above is a very weak argument. In particular, since PredPol only works on essentially aggregate counts of crime incident the composition of the synthetic population should not matter. However, next we will see a way to each squash this very weak objection.
Theoretical modeling of feedback loops
Acknowledgments
The arguments in this section are heavily based on a FAT* 2018 paper by Ensign, Friedler, Neville, Scheidegger and Venkatasubramanian.
One potential nitpick with simulation results is that they are simulations and e.g. do not guarantee that the observed result would necessarily hold in situations not covered in the simulations. In particular, we would like to argue that under some fairly general conditions feedback loops can exist. More specifically, we would like to argue that no matter what the specific population looks like as long as the general conditions holds, then a feedback loop exists. The above statement is not possible to prove using simulation results since simulations cannot cover all possibilities.
In this section, we will consider a theoretical model to mathematically prove that under some fairly generally conditions, feedback loops always exist. The catch is that to prove theorems one typically has to make simplifying assumptions in the theoretical model. Thus we being by stating the assumptions we will consider in this section (this is only one of the many settings that Ensign, Friedler, Neville, Scheidegger and Venkatasubramanian consider in their paper.
Basic setup
We will assume that there are only two regions we are interested in-- $E$ (for East side in Buffalo and $W$ (for (Upper) West side in Buffalo ).
We will assume there is only one cop tasked with patrolling $E$ and $W$. Further, given that only one cop is patrolling an area we assume that in one day the cop can only discover (at most) one crime (there is paperwork etc. involved and with one cop patrolling these big areas the chances of them catching multiple crimes are pretty-much non-existent.
These are indeed NOT realistic assumptions. But we make these assumptions since it makes proving things in this model easier. The way to look at this model is that this is a first attempt and indeed followup modeling would be needed to make the model more realistic.
Assumption 1 (assigning the cop to a region)
We will assume that the cop can only go to one region each day. (If you are OK with the assumption of there being only one cop, this is not that unrealistic!)
Further, we will assume that the cop will visit a region with probability directly proportional to how many crimes have been reported till date in the given region.
Notation alert
For any given day $t$, we will use $n^{(t)}_E$ and $n^{(t)}_W$ to denote the number of observed crimes in $E$ and $W$ respectively from day $0$ to day $t$.
In particular, the cop will visit $E$ with probability \[\frac{n^{(t)}_E}{n^{(t)}_E+n^{(t)}_W}\] and will visit $W$ with probability \[\frac{n^{(t)}_W}{n^{(t)}_E+n^{(t)}_W}.\]
Assumption 2 (unequal crime rates)
We will assume that the $E$ and $W$ have different crime rates (which are unknown).
Notation alert
The crime rate for $E$ is $\lambda_E$ and the crime rate for $W$ is $\lambda_W$.
In particular, we are assuming \[\lambda_E\ne \lambda_W.\] Note that we are not assuming that the rates are widely different. E.g. $\lambda_E=10.5\%$ and $\lambda_W=11\%$ are perfectly allowed in the model.
Assumption 3 (observed crime rate = actual crime rate)
We will assume that crime is discovered by the cop in either region EXACTLY with the same probability as its actual crime rate.
NOT a realistic assumption
As we have seen before this is not a realistic assumption.
However, as we will see shortly even under this very generous (to PredPol) assumption, we will show the existence of a feedback loop, which only makes the argument for dangers of feedback loop stronger.
In particular, if the cop goes to $E$, then they will observe one crime with probability $\lambda_E$ and no crimes with probability $1-\lambda_E$. Similarly if the cop goes to $W$, then they will observe one crime with probability $\lambda_W$ and no crimes with probability $1-\lambda_W$.
Exercise
Given the above what are the relationships of $n^{(t+1)}_E$ with $n^{(t)}_E$ (and similarly the relationship of $n^{(t+1)}_W$ with $n^{(t)}_W$)?
If the cop visits $E$ with probability $\lambda_E$ the cop will discover/report one crime and not crime otherwise. In other words, \[n^{(t+1)}_E = \begin{cases} n^{(t)}_E+1 & \text{ with probability } \lambda_E\\ n^{(t)}_E & \text{ with probability } 1-\lambda_E \end{cases}. \]
And we have a similar result If the cop visits $W$: \[n^{(t+1)}_W = \begin{cases} n^{(t)}_W+1 & \text{ with probability } \lambda_W\\ n^{(t)}_W & \text{ with probability } 1-\lambda_W \end{cases}. \]
Now that we have listed all our assumptions, we actually have fully specified the model. Below we re-state the model as how the values $n^{(t)}_E$ and $n^{(t)}_W$ change over time:
The evolution of the number of observed crimes
- The process starts with initial values $n^{(0)}_E$ and $n^{(0)}_W$.
- For $t=1,2,\dots$
//The process repeats "forever"
- With probability $\frac{n^{(t)}_E}{n^{(t)}_E+n^{(t)}_W}$ do:
//Cop visits E
- With probability $\lambda_E$ set $n^{(t+1)}_E =n^{(t)}_E+1$
- Else with probability $1-\lambda_E$ set $n^{(t+1)}_E =n^{(t)}_E$
- Otherwise with probability $\frac{n^{(t)}_W}{n^{(t)}_E+n^{(t)}_W}$ do:
//Cop visits W
- With probability $\lambda_W$ set $n^{(t+1)}_W =n^{(t)}_W+1$
- Else with probability $1-\lambda_W$ set $n^{(t+1)}_W =n^{(t)}_W$
- With probability $\frac{n^{(t)}_E}{n^{(t)}_E+n^{(t)}_W}$ do:
OK, so we go into the weeds of the model for a bit. Let us go backup and make sure we understand what outcome could correspond to a feedback loop in this model:
Exercise
To make things concrete assume that $n^{(0)}_E= n^{(0)}_W=100$ and $\lambda_E=10.5\%$ and $\lambda_W=11\%$. What would you consider to be a manifestation of feedback loop as the process above runs?
Hint: Think about how the ratios $\frac{n^{(t)}_E}{n^{(t)}_E+n^{(t)}_W}$ and $\frac{n^{(t)}_W}{n^{(t)}_E+n^{(t)}_W}$ evolve as $t$ grows larger. (Side question: why are these ratios something worth monitoring?)
First note that the ratios $\frac{n^{(t)}_E}{n^{(t)}_E+n^{(t)}_W}$ and $\frac{n^{(t)}_W}{n^{(t)}_E+n^{(t)}_W}$ are the probabilities that the cop goes to $E$ and $W$ on day $t$ respectively. Ideally, one would like these probabilities to be proportional to $\lambda_E$ and $\lambda_W$ respectively.
Since $\lambda_E$ and $\lambda_W$ are very close to each other, a feedback loop could be said to exist if in the steady state the probability that the cop goes to $E$ is not close to the probability that they go to $W$. For example, an extreme case of feedback loop will occur if the cop almost surely goes to only one region.
Existence of feedback loop (and a fix)
We will very briefly argue why a feedback loop exists in the model above and how one might go about fixing it. We refer the interested reader to the paper by Ensign, Friedler, Neville, Scheidegger and Venkatasubramanian for more details (including they prove the existence of the feedback loop).
Feedback loop always exists
It can be shown that if $\lambda_E\gt \lambda_W$, then the cop will go to $E$ with probability $1$ and if $\lambda_W\gt \lambda_E$, then the cop will go to $W$ with probability $1$. In other words, if there is any imbalance (however slight) between the crime rates in $E$ and $W$, eventually the cop will only go to the region with the higher crime rate.
Exercise
Can you argue the above claim?
Here is the intuitive argument. Assume that $\lambda_E\gt\lambda_W$ (the argument for the other case of $\lambda_W\gt\lambda_E$ is essentially the same), then assuming the cop goes to a specific region, the number of observed crimes in $E$ will be more than $W$. And after each day passes this "advantage" is re-inforced till cop only ends up going to $E$.
This result can be mathematically proven using Polya's urn model . In an tangentially related item, here is cool video on using Polya' urn to verify election results:
A potential fix
In the above model, Ensign, Friedler, Neville, Scheidegger and Venkatasubramanian suggest the following fix (which they can mathematically prove that it works) is based roughly on the following idea. If the cop visits a specific region most of the time, then it should not be a surprise if they discover a crime in the region and in such a case they should "discount" the crime discovery by not recording such discovery most of the time. On the other hand, if the cop visits region infrequently and they discover a crime, they have learned something "new" and hence would record such crime discoveries most of the time.