The Problem

This problem is just to get you thinking about graphs and get more practice with proofs.

A forest with $c$ components is a graph that is the union of $c$ disjoint trees. The figure below shows for an example with $c=3$ and $n=13$ with the three connected components colored blue, read and yellow).

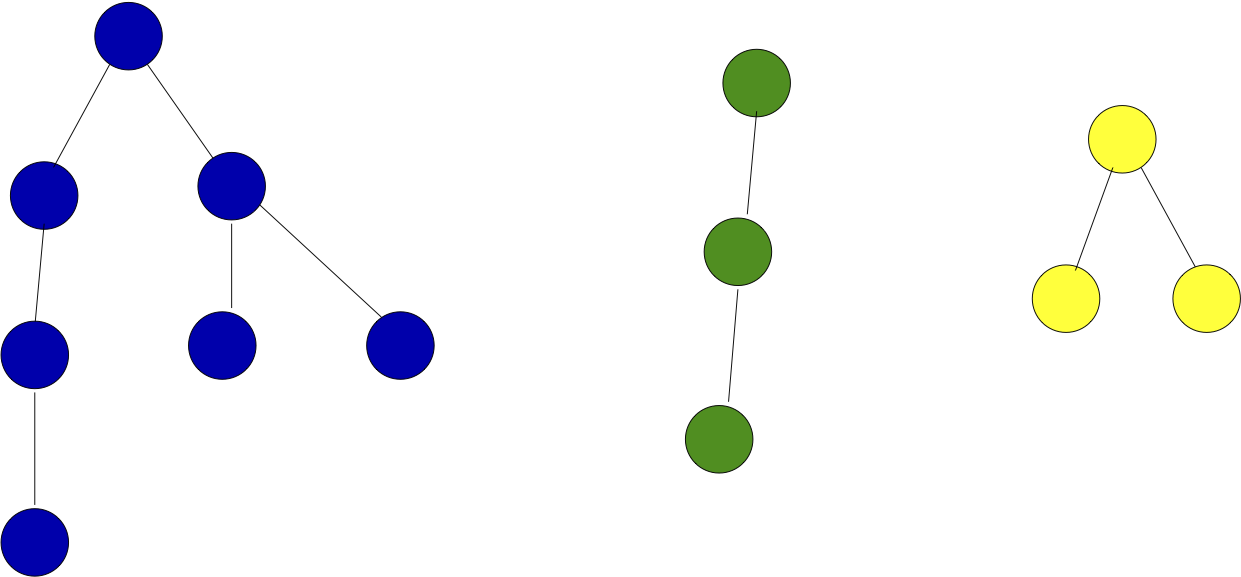
Prove that an $n$-vertex forest with $c$ components has $n-c$ edges.

The Problem

There is a group of $p$ Ava DuVernay fans (or ADFs for short) who have booked an entire movie theater for a screening of A Wrinkle in Time . Out of the $p(p-1)/2$ possible pairs, $f$ pairs of ADFs are friends. The movie theater is called the Square Theater and has $p$ rows with each row having exactly $p$ chairs in them. (If it helps, you can assume that the $p^2$ chairs are arranged in a "grid"/"matrix" form where each of the $p$ rows has $p$ chairs each and each of the $p$ columns has $p$ chairs each.)

The ADF organization committee has come to you to help them efficiently solve the following seating problem for them. Informally, you want to seat the ADFs so that friends can talk to each other (and "distant" friends remain distant). Next, we make this informal description more formal.

A seating (as you might expect) is an assignment of the $p$ ADFs to the $p^2$ chairs in the theater so that each ADF gets his/her own chair.

A seating is called admissible if

1. for every pair of friends $(b_1,b_2)$, they can talk to each other during the movies
2. some ADF is assigned a seat in the first row and
3. the seating satisfies the distance compatible property.

The ADFs have been to the Square theater before so they have figured out that two people can talk to each other if and only if they are either

• seated in the same row or
• are seated in the rows next to them (i.e. either to the row directly in front or the row directly behind. The first and the last row of course only have one row next to them).

A seating has the distance compatible property if and only if the following holds. For any $b_1$ who is assigned a seat in the first row and any ADF $b_2$, if $b_1$ and $b_2$ have a friendship distance of $d$ (assuming $d$ is defined), then they have to be seated $d$ or more rows apart. (The friendship distance is the natural definition. Let a friendship path between $b_1$ and $b_2$ be the sequence of ADFs $f_0=b_1,f_1,\dots,f_{k-1},f_k=b_2$ (for some $k\ge 0$) such that for every $0\le i\le k-1$, $(f_i,f_{i+1})$ are friends-- the length of such a path is $k$. The friendship distance between $b_1$ and $b_2$ is the shortest length of any friendship path between them. So if $b_1$ is $b_2$'s friend, they have a friendship distance of $1$ and if $b_2$ is a friend of a friend, they have a distance of $2$ and so on. The friendship distance is not defined if there is no friendship path between $b_1$ and $b_2$.)

As an example consider the case of $p=3$ and $f=2$ as follows. The ADFs are $A,B,C$ and the $(A,B)$ and $(B,C)$ are the pairs of friends. Then an admissible seating is to assign the "left-most" seat on first row to $A$, the left-most seat in second row to $B$ and the left-most seat on the third row to $C$. This following is also an admissible seating: $B$ is assigned (any seat) in the first row while $A$ and $C$ are assigned any two seats in the second row.

Your final task is to design an $O(f+p^2)$ time algorithm that computes an admissible seating, given as input the set of $p$ ADFs and the set of $f$ pairs of ADFs who are friends. Here are the two parts:

• Part (a): Formalize the problem above in terms of graphs: i.e. write down
  1. How you would represent the input as a graph $G$;
  2. How you would define a seating and
  3. Define what it means for a seating to be admissible in terms of properties of graph $G$.
• Part (b): Using part 1 or otherwise design an $O(f+p^2)$ time algorithm to compute an admissible seating. (Recall that your algorithm should work for any set of $p$ people and any possible set of $f$ friendships.) You should prove the correctness of your algorithm. You also need justify the running time of your algorithm.

  Hint

  Think how you can use some of the graph exploration algorithms we have seen in class.

  Common Mistake

  A common mistake in this (and related) problem is to think that both BFS and DFS are completely interchangeable. There are concrete cases where they are not.

The Problem

A 4-clique in a graph $G=(V,E)$ is a set of four distinct vertices $\{u,v,w,x\}$ such that $(u,v),(v,w),(w,x),(x,u),(u,w),(v,x)\in E$. (Note that $G$ is undirected.) In this problem you will design a series of algorithms that given a connected graph $G$ as input, lists all the $4$-cliques in $G$. (It is fine to list one $4$-clique more than once.) We call this the 4-clique listing problem (duh!). You can assume that as input you are given $G$ in both the adjacency matrix and adjacency list format. For this problem you can also assume that $G$ is connected.

Below are the two parts of the problem:

• Part (a): Present an $O(n^4)$ time algorithm to solve the $4$-clique listing problem.

  Note

  The trivial algorithm works. For this part only a correct algorithm idea is needed.

• Part (b): Present an $O(m^2)$ algorithm to solve the $4$-clique listing problem.

The Problem

In this problem we will explore graphs and problems that are relatable to the 6 degrees of separation problem, which claims that everyone in the world is connected by 6 people or less. We will investigate different networks to see the minimum distance between some starting node, s, and all other nodes in the graph. We will be using real-life data sets to test your code.

We are given a starting node $s$ for some undirected graph $G$ with $n$ nodes. The graph is formatted as an adjacency list, meaning that for each node, $u$, we can access all of $u$'s neighbors. The goal is to output all $n$ nodes in $G$ along each $u$'s minimum distance from $s$.

Input

The input file is given with the first line as the starting node and the remainder of the file is an adjacency list for graph $G$ (we assume that the set of vertices is $\{0,1,\dots,n-1\}$). The adjacency list assumes that the current node is the index of the line under consideration. For instance line 0 of the input file (not including the starting node) has the list of all nodes adjacent to node 0.

                s		<- Starting node (some node between u0 and un-1)
                u1 u4 u6		<- All nodes that share edges with u0
            	u3 uu		<- All nodes that share edges with u1
		u0		<- All nodes that share edges with u2
		.
		.
		.
		u0 u4 u2 u7 	<- All nodes that share edges with un-1
	    

For example

            	2		<- Starting node
	 	1 2		<- Node 0 shares edges with nodes 1 & 2
		0 3    		<- Node 1 shares edges with nodes 0 & 3
	    	0 3 4 5		<- Node 2 shares edges with nodes 0, 3, 4 & 5
		1 2 6 7		<- Node 3 shares edges with nodes 1, 2, 6 & 7
		2		<- Node 4 shares edges with node 2
		2		<- Node 5 shares an edge with node 2
		3 8		<- Node 6 shares an edge with nodes 3 & 8
		3 8		<- Node 7 shares edges with nodes 3 & 8
		6 7		<- Node 8 shares edges with nodes 6 & 7
	    

If we draw the graph using the above input, it will look like this:

Output

The output is every node (given by the index in the array), along with it's minimum distance from the starting node formatted as your language of choice's array-type data structure (see below for the exact details).

            	[d0 d1 d2... dm]   					<- Node 0 is distance d0 from the starting node
									   Node 1 is distance d1 from the starting node
									   Node 2 is distance d2 from the starting node
									   .
									   .
									   .
									   Node m is distance dm from the starting node
	    

For example, using the example input from above:

           	[1, 2, 0, 1, 1, 1, 2, 2, 3]			<- Node 0 is distance 1 from node 2
								   Node 1 is distance 2 from node 2
								   Node 2 is distance 0 from itself 
								   Node 3 is distance 1 from node 2 
								   Node 4 is distance 1 from node 2
								   Node 5 is distance 1 from node 2
								   Node 6 is distance 2 from node 2
							 	   Node 7 is distance 2 from node 2
								   Node 8 is distance 3 from node 2