ML models
This page talks in more detail about ML models and gives more technical details on some of the common model classes.
-
I am not saying asking such a question could have made the task of figuring out the location of
yany easier but more that asking a more complicated question like this is not on the table. -
It is well-known that a binary tree with
n-1internal nodes hasnleaf nodes but if you are not familiar with this result, just take this as a given. -
Well, it is not that involved but it is much easier to follow if one is familiar with linear algebra (matrices and vectors). However, we do not assume such knowledge in this course.
-
Otherwise why would anyone study neural networks as a separate model class from linear models? :-)
Under Construction
This page is still under construction. In particular, nothing here is final while this sign still remains here.
A Request
I know I am biased in favor of references that appear in the computer science literature. If you think I am missing a relevant reference (outside or even within CS), please email it to me.
Background and a simplification
Recall that we are in the seventh step in the ML pipeline:

Focus on two input variables
For ease of exposition we will restrict most of the discussion in these notes to the case when there are two input variables that we will consider. In "real-life" one has to consider more variables (and we will shortly see a mathematical reason for this) but dealing with two variables means that we can use 2D-plots which makes visualization easier.
The default setup
To ground most of the discussion in these notes in something concrete, let us consider the situation where you are trying to predict risk for heart disease based on simple to measure/collect characteristics (also called risk factors, which we will call input variables to be consistent with how we have talked about variables we use to predict the target variable (which in this case is risk of heart disease)). You first start off with the case when the two input variables are weight (which in the data representation step was decided to be measured in kilograms) and height (which in the data representation step was decided to be measured in centimeters). Based on the tallest and heaviest human in recorded history, the pairs of all feasible $($weight,height$)$ pairs fall in the gray shaded region in this plot:

Now we can map every human on earth to a point within this shaded region. E.g. below is how it plays out for me:

My numbers are not exact
In case a third party broker wants to use the above information about my weight and height: the above are not my exact height and weight. They both have some fudge factor added to them (but I will not say what those fudge factors are!). Note that this affects some of the numbers about me that would be calculated later in these notes.
Can we really maps all humans to a unique point?
We claimed above that we can map every human on earth to a point in the shaded region. While this is correct, we claim that not every human gets mapped to a unique point. We will actually argue this using a simple yet surprisingly effective mathematical argument called the pigeonhole principle . We will not need the general statement of the principle but if you are curious, here is a video with more (mathematical) details:
Back to the question at hand. Assume that we are measuring weight in increments of $1$ kg (in case you are curious, human weight changes more than that in one day so this precision seem reasonable) and let us assume that the height is measured in $0.1$ cm increments. Thus, we have $700$ distinct possible weights and $3000$ distinct possible heights. Thus, the total number of distinct $($weight,height$)$ pairs is $700\times 3000$, which is $2.1$ million possibilities. However, the current human population is over $7.7$ billion people. Since there are more people than the number of distinct $($weight,height$)$ pairs, there has to be at least two humans with the same $($weight,height$)$ pairs. In fact, you can also argue that at least $3000$ humans with have the same $($weight,height$)$ pair.
The above shows that the mapping of all humans to $($weight,height$)$ pairs is not ideal since there are many "clashes." Ideally, we would like to map humans to sequence of numbers so that everyone gets a unique sequence. This is easier to do when we use more than two variables (since then at least the total number of possible sequence of data values would be more than the human population). And indeed in real life ML systems, each human is mapped to many more input variables. In this case, each human will get mapped to a point in higher dimensional space. For example, in our current example, let us say you decide to add age as another risk factor/input variable. In this case we can envision each human being mapped to 3D-space and here is where I land up in this space:

What is a model class?
Recall that we have seen the notion of a model before but we will spend more time on the notion (and more specifically on the notion of a model class).
Binary Classification is the name of the game
We had mentioned this in the passing earlier, that in this course we will focus on binary classification. In other words, the target variables that we will consider in this course only take two values: typically we will call one value positive and the other negative. For example, in the running example in this notes of predicting the risk of heart disease, positive would mean high risk of getting heart disease and negative would mean low risk of heart disease.
Of course, it many cases (including the heart disease risk prediction) it makes sense to have the target variable take many values (or even for the case when the target variable is inherently binary it makes sense to assign a probability of whether the target variable is positive-- in which case the target variable is a real number between $0$ and $1$ and thus takes on infinitely possible values).
We decided to focus on binary classification since it makes the exposition easier (including drawing figures of the kind y'all will see soon) but at the same time is complex enough to illustrate many of the technical details and nuances.
Back to models
While we have alluded to a model before (and e.g. delved into it before with some examples), let us go over the concept again. Simply put, for binary classification and for the case of two variables, a model is a "curve" that divides the set of pairs of points into what it deems to be positive and what is deems to be negative.
The color scheme
We will color points in a dataset as green or red depending on whether they are labeled as positive or negative. However, for clarity, points that are deemed to be positive by a model will be colored blue and those deemed to be negative will be colors yellow.
This color scheme is not standard and is something that I decided on (for reasons that I cannot remember now...).
Coming back to the example of risk of heart disease with weight and height as input variables, here is a potential model:

Note that by the time we have at the stage of picking a model (class) we have already fixed the data representation (and hence we have limited the domain of all possible values-- denoted by gray for the running example earlier), then the model above is pretty much defined by the blue line above. The reason the line is not equivalent to the model is because we could flip what the model thinks of as positive and negative points, like so

Linear models
The models we considered above (as we have seen before) are called linear models (because you can literally draw a line to present them in 2D). In particular, in the case of two input variables, a linear model is completely defined once you specify the line as which of the two sides is the positive side (and the other side automatically becomes the negative side).
Perceptron by another name
In case you are interested/care, what we call linear model above is called the preceptron in the machine learning literature.
The early work on Perceptrons was actually done right here in Buffalo! .
However, there is no restriction that the only models we can consider are liner models. In particular, much of the recent advances in ML have been due to the use of "non-linear" models. E.g. in our running example, we could have a model like this where we still have a positive and a negative region but the boundary is no longer a line (but a more non-trivial curve):



The figures above are not of real models
In case y'all were wondering the non-linear models were all drawn by hand and do not correspond to a model that has been used by someone in real life. However, except for perhaps the last figure, they are approximations of models that are used in real-life.
At this point, however, we are ready to be more specific on what we consider to be a model:
Models for binary classification
A model is a function (or a procedure if you will) that divides up the ambient space (in the running example it is the gray area in the first figure) into disjoint regions where each region is colored blue (for what the model considers the positive points) and yellow (for what the model considers to be negative points).
One specific model is not enough
Independence of model from problem/data
When we first looked at choosing the model class as part of our walkthrough of the ML pipeline, by the time we looked at the linear model cartoon, we already had the labeled (red/green) points. However, so far we have not seen labeled points in our plots yet. Why so?
The fact that you can talk about a model independent of the training data is precisely the reason ML is so effective: i.e. traditionally it has been important for the models to be defined independently of the problem/data so that one can reason about them independently of the problem/data. This abstraction is what gives ML its power. In particular, this abstraction allows one to use the same technology for different problems/data and allows for the wide-spread use of ML in many areas. Basically if one can do the seventh step of the ML pipeline (and beyond) independently of the first six steps, then one can use "off-the-shelf" ML systems for the seventh step and beyond of the ML pipeline and for a particular application, one can just concentrate on the problem-specific tasks. In particular, any advance in the non-problem specific steps of the ML pipeline can then be used for any problem where one has handled the first six steps.
As mentioned above, the argument above is the current/traditional way ML systems are used. However, as we will see later in the course, such a clean separation between the first six steps of the ML pipeline and rest leads to situations with non-ideal outcome especially when it comes to questions of fairness or bias. The high-level reason for this is that even though we have drawn the ML pipeline as a sequential set of steps, in real life they are not so. Specifically, the fact that every step of the ML interacts with society means that the various are not independent of each other even though our flowchart might make it look otherwise.
Let us now consider a set of $10$ labeled data points (where recall green is positive and red means negative labels):





Perhaps a linear model and its complement is enough for all cases?
Given what we have seen so far, it is clear that we cannot have a single linear model that can explain all possible datasets. However, the following possibility remains: from what we have seen so far, perhaps we can get always by choosing a single line but we might have to freedom in which part is the blue region and which part of the yellow region?
Before you move on, think by yourself what you think the answer is to the above question.
Perhaps not surprisingly, the answer to the above question is no. In particular, consider the following six different datasets:

Convince yourself
Convince yourself that the two linear models we have considered so far only correctly classify each of the ten points in one dataset and misclassify at least two points in each other dataset (i.e. for each of the five datasets each of the two linear models have at least $20\%$ error.

Exercise
Figure out what is the smallest error that a model makes on a dataset other than its corresponding one.
What we need is a class of models
Hopefully by now you are convinced that a single (linear) model is not enough to represent multiple datasets. This implies that we will need multiple models: i.e. we need a class of models, like so from the examples above:

Two Questions
You might be asking yourself the following questions (if not, you should!):
- Are linear models enough to "capture" all possible datasets?
- How should we define the class of (linear) models? E.g. would the six linear models be enough? If not, would $100$ suffice? What about a million? A billion? Should we consider infinitely many linear models?
The answer to the above question is no. Consider e.g. the following four datasets (with more than $10$ points in the previous examples):

Exercise
Convince yourself that no linear model can correctly classify all points in any of the four datasets above.
Indeed the above four datasets were generated so that non-linear models perfectly fit them:

What should constitute a model class?
We now return to the second question we asked above. For simplicity, we focus on linear models in this part (though the general ideas hold for non-linear models as well).
Exercise
Convince yourself that having a finite set of linear models will not be able to capture all datasets that can indeed fit a linear model (for the time being ignore precision constraints: i.e. assume we can represent any number to arbitrary precision).
Hint: If you pick a finite set of linear models. Since there are infinitely many possible lines (for a more rigorous argument on this see the section on linear models). This means that your finite class will not represent a linear model. Can you use this linear model to construct a dataset that cannot be perfectly fit with the finite number of linear models in your class.
The above exercise implies that we need to have infinitely many linear models in our notion of the class of linear models: in fact, the argument also shows that we have to include all possible linear models. However, this leads to the following potential bottleneck for the future steps of model training:
How do we search among infinitely linear models?
Given that we have argued that we should consider infinite set of all linear models, when it comes to the model training step, how can we hope to search among infinitely many linear models to find the best fit for a given dataset?
The short answer is that we don't!. it turns out that for linear models, given a dataset there is a closed-form expression to figure out the best linear model-- in particular, this translates into an efficient algorithm (in the traditional sense!), which given a dataset outputs the best (in a precise mathematical sense) linear model for the given dataset. We will come back to this later in these notes.
A natural followup question is whether we can also learn the best non-linear model that fits any given dataset? The answer is yes and no:
Why Yes?
Convince yourself that given any dataset there is always a (possibly non-linear) model that fits it perfectly. Assume here there are not two datapoints with the same input variable values but with different labels. E.g. in our running risk of heart disease example this means that there cannot be two humans with the same weight and height pair but one of them has high risk of heart disease while the other has low risk of heart disease.
Hint:Given a dataset, can you use the dataset itself to define the model fits it perfectly? (Do not worry about how complicated the resulting model will be-- you just need to argue that such a model exists.) And do not peek below before you have spent some time thinking about the answer :-)
Why No?
It turns out that one answer to the question above is to use the labeling of the dataset to define the model itself. One (of the many) issues with "solution" is that the "complexity" of the model depends on the dataset itself. In particular, in general the best representation of such a model is the set of points itself. When your dataset has millions of points, this is not a very efficient representation.
What do we need from a model class?
We have mentioned some of the desirable properties of a model class in passing above. Finally, we collect some of the desirable properties of a model class before we delve into some specific model classes.
Parsimonious representation
We would like our model class to have its representation size not depend on the size of the dataset (or has a more reasonable dependence than having to store the entire dataset to figure out the best fitting model.
In addition, models with small representation size can be considered to be the "right" model based on the Occam's razor , which says that the simplest explanation is probably the best solution. This is also related to the notion of generalization (which we have briefly seen before).
It turns out that all the model classes that are used in an ML pipeline have these properties (though the notion of "small" changes from class to class).
Efficient model training
In the later step in the ML pipeline of model training, the technical task is the following: given a dataset, figure out the best fit model from the given class. Of course, we would like to be able to do this step efficiently.
And it turns out that while sometimes it is possible to figure out the optimal model that fits a given dataset efficiently (e.g. linear models), this is not always possible (e.g. for neural networks). In the latter case, we often try to compute an approximately optimal model: i.e. while we might not find a model that has the smallest possible misclassification error, we might be able to find a model that makes few more misclassification errors.
In particular, one way is to replace the objective of minimizing the number of errors when figuring the best (linear) model and replacing it with a weaker loss function: i.e. instead of straight-up counting on how many training data points a model makes an error, one uses a more generic function that also takes into account the extent to which the model makes an error on a data point. It would seem like this would make model training even harder but because of mathematical reasons as long as these loss functions have some "smoothness" properties, then one can carry out the model training step efficiently. We will come back to this later on in these notes (and the course).
Efficient prediction
In the later step in the ML pipeline of prediction, the technical task is the following: given a point and a specific model, figure out the label the model will assign to the point. Of course, we would like to be able to do this step efficiently.
We would like to point out that model training is basically done once while prediction is done over and over again once the training is done. Hence, while we want both efficient training and prediction, the notion of "efficient" is different for both tasks. E.g. in some cases, it is not unreasonable to spend days trying to do model training but the corresponding prediction has to be done in (fraction of) a second.
The above seems good but we claim that there is a trivial model class that satisfies all properties above:
Trivial model class
Can you think of a trivial model class that satisfies all the properties above?
Hint: What is the simplest model class that you can think of? Another hint: do not worry about how accurate your model will be.
As shown by the above example, the above properties are useless with the model being powerful enough to faithfully represent various datasets:
Model expressivity
What is missing from the above properties is any constraint on how good the model class is at predicting datasets? In other words, for "real life" data, how accurately can this model class predict the correct labels?
The quotes around "real life" data is on purpose: it is a fool's errand to try and precisely define what real life data looks like. There are two ways around this: to propose certain natural conditions on the data and then theoretically show that under these theoretical conditions on the data, the best model in your class will predict the data labels with small error (and presumably you also experimentally show that at least some representative datasets satisfy the theoretical conditions). Alternatively, you run experiments and show that on some representative datasets the empirical prediction errors of the best model in your class is small.
While we will not talk about this now, there could be other desirable properties:
Other desirable properties?
As we progress in the course, we will see that there are properties other than the ones above (which are the primary focus of traditional ML) that could be useful. E.g. does the model make it easy to "explain" its decision to a human? Can we argue that in some precise sense the model is "fair" or not "biased."
Can you think of other useful properties?
Next, we consider three specific model classes (where among others we will pay special attention to the three desirable properties above). We will have the most detailed treatment of linear models: detailed treatment of decision trees and neural networks is out of the scope of this course.
Linear model
Recall that we have already defined linear models for two variables. We will re-define linear models more formally soon, but for the time being let us consider an even more special case of linear models: we will consider the case where there is only one input variable.
The case of one input variable
A natural first question is whether using a single input variable ever be useful in our quest. The answer does turn out to be yes (but for trivial reasons):
Exercise
Given a specific target variable (e.g. in our running example whether a human has a high or low risk of heart disease) can we even hope to predict it with a single input variable?.
Hint: Given a target variable, can you think of a variable that can predict it (perfectly)? (If you think the answer is trivial, you are correct :-)). Think about it yourself first before peeking below!
What if input variable cannot be the target variable?
Now let us consider the more realistic setup where the single input variable cannot be the same as the target variable and has to be something that can be directly measured. E.g. in our running example of predicting heart disease this input variable has to be something that can be measured from humans easily.
It turns out that indeed there is such an input variable (and it is related to the two variables of weight and height that we have considered so far) and further, this has been studied extensively before.
Assumption for the rest of the course
For the rest of the course, we will assume that we do not have direct access to the target variable. In particular, none of the input variables can be the target variable.
Body Mass Index
The Body Mass Index (or BMI) is defined as follows. Let $w$ and $h$ be the weight and height of someone in kilograms and centimeters respectively (as we have seen so far). Then their BMI $b$ is defined as follows: \[b=\frac{w}{\left(\frac h{100}\right)^2}.\] This is equivalent to the more prevalent definition: BMI is the ratio of the weight in Kgs to the square of weight in meters.
As mentioned earlier, BMI has been used extensively as a "risk factor." E.g. here is a relatively recent finding on the connection between BMI and risk of heart disease:
It would be remiss of me to not mention that BMI however by itself is not a perfect measure for everyone:
In case you are interested, here is the distribution of BMI among US populations from this page on BMI (which also has other infographics in case you are interested):

Linear models for one variable
Why consider linear model for single variable?
Given the comment above that using one variable make accuracy of prediction potentially worse (and in practice this is almost always the case), then why are we considering linear models in one variable? We are mainly doing this because it simplifies the math but still allows for interesting discussion. We will come back to this when we talk about training of linear models in two variables.
We will continue our example of heart disease risk and note that we have gone down from two variables (weight and height) to one (BMI), like so:

Linear model for single variable $b$
After a moment's thought one can see that for one variable (say our BMI variable $b$) a linear model consists of specifying a special value (call it $b^*$ in our example) and then specifying if all the points to the "left" of $b^*$ are blue or yellow, like so:

In fact, the way CDC designates heart disease risk (among other health risks) based om BMI does exactly this (where recall blue is high risk for heart disease and yellow is low risk):

If you like your models served mathematically, here is how the prediction of the linear model $\ell$ is defined given a BMI value $b$ (where $1$ denotes positive label (or blue color) and $-1$ denotes negative label (or yellow color)): \[\ell(b)=\begin{cases} 1 & \text{ if } b\lt b^*\\ -1 & \text{ if } b\ge b^* \end{cases}.\] Note that the above corresponds to the linear model in the left figure above: to get the linear model in the right above figure just swap the $1$ and $-1$ in the definition above.
Give it a moment's thought...
If you do not see why a linear model in one input variable will have the form as mentioned above, now would be a good time to think more about it or ask about it in class.
Properties of linear models in single variable
Next, we go through the desired model class properties for linear models for single variable.
Parsimonious representation
Let us look back at the definition of linear model on one variable $b$. Note that to define a linear model on $b$, we need to define two things:
- The "threshold" value $b^*$ and
- Which "side" of $b^*$ ("left" or "right") corresponds to blue color (the other side automatically gets assigned the yellow color).
In other words, we just need two parameters to represent the entire class of linear models on single variables. In some sense this is basically the best we can hope for! However, there is a potential issue.
Exercise
One might question that even though $b^*$ is one parameter, how much precision would we need to represent $b^*$? For example, technically BMI is a real number so $b^*$ can take infinitely many values. However, there is an easy way out of this, which leads to the actual exercise.
The way out of the conundrum is that even though $b^*$ can potentially take infinite values, we only care about the actual value of $b^*$ once we have a dataset. For notational simplicity, let us assume that the $n$ points in the dataset are $b_1,b_2,\dots,b_n$ where each $b_i$ is BMI value of the "$i$th" person and they are in increasing order, i.e. $b_1\le b_2\le \cdots\le b_n$. OK, now that we have set up our notation, time for the actual exercise!
Consider any index $i$ such that $1\le i\lt n$ and $b_i\lt b_{i+1}$ (if they are the same then you can ignore such an $i$). Now argue that for all potential values of $b^*$ such that $b^*\gt b_i$ and $b^*\lt b_{i+1}$ the corresponding linear model colors each of the $n$ points in exactly the same way.
Hint: This figure might be helpful with the above (ignore the actual label of the dataset points and look at how the two possible values of $b^*$ (denoted by the two vertical lines) corresponding to two technically different linear models assign colors to the $n$ points in the dataset:

From the above or otherwise, conclude that for model training one only needs to consider the possible values of $b^*$ from the numbers $b_1,\dots,b_n$-- i.e. we need to only consider $n$ possible values (instead of infinitely many possible values) for $b^*$ during the model training step.
Efficient model training
Let us first start with the error function that we have seen so far: we want to minimize the number of points that are misclassified by our linear model in one variable.
It turns out that most of the heavy-lifting we have already done in the previous property itself. Since that are only $n$ possibilities for $b^*$, we can just "brute-force" it-- i.e. for each of the $n$ choices of $b^*=b_i$, we figure out how many points are misclassified and keep track of these $n$ error values. Finally, we pick the $b^*$ with the smallest error value.
The above algorithm (again in the traditional sense!) spends roughly $n$ steps on each choice of $b^*$ and since there are $n$ choices, the algorithm overall takes roughly $n^2$ steps. While this is fine for small datasets, for datasets with millions of points this is much slower. Next, we see that how we can do the same in roughly $n$ steps:
Exercise
The main observation is that if instead of maintaining the total number of errors for each choice of $b^*=b_i$, if we keep track of number of errors on both sides of $b_i$-- call the number of errors on the left of $b^*$ to be $e_L$ and that to the right be $e_R$ (note that we finally only care about $e_L+e_R$ but it helps to maintain this extra state). Now argue the following.
Argue that if we know the values of $e_L$ and $e_R$ when we choose $b^*=b_{i+1}$, then those values can be updated with constant many steps.
Hint: Argue that only the classifications of $b_{i+1}$ changes when we change $b^*$ from $b_i$ to $b_{i+1}$, see e.g. this figure:

We now remind the reader that all of the above algorithms are for the case when the error function only counts the number of mistakes but does not take into account the "magnitude" of the error (in particular, how "far" is a misclassified point from $b^*$). The latter error model also makes sense (and is considered more "robust"). We will return to the question on how to efficiently train linear models in one variable for this error model later on.
Efficient prediction
This basically follows from definition so we leave it as an exercise:
Exercise
Once the linear model $\ell$ (i.e. the threshold $b^*$ and which side is the blue color) is fixed, then given a point $b$ determining its label $\ell(b)$ can be done in constant many steps.
Model expressivity
We will not spend much time on this aspect except to point out unless the dataset is really close to explained by a linear model, a linear model will not be able to fit a more complicated dataset (and we have seen examples above where the points were essentially generated from a "non-linear" model). This is why in state-of-the-art ML pipeline, where accuracy is the primary objective, use non-linear models.
Other desirable properties
We will talk about this in more detail later on in the course but we would like to mention why linear models (even in one variable) are used in assessing risk of certain common diseases. This is because it is easier for a doctor to explain why the patient is at a higher risk for heart disease according to the model. Of course the doctor will not talk in terms of a model but will say something along the lines of "Your BMI is above $30$, which according to studies, means you are at higher risk of getting a heart attack."
Linear models on two variables
We now consider the case of linear models with two variables.
A diversion
If you do not remember what linear models in general were then good: don't try to remember it. If you do remember what a linear model is, try to play along :-)
Recall that for linear hash on one variable $b$ was defined by deciding on a threshold $b^*$ and then deciding which "side" was positive and negative. Mathematically, \[\ell(b)=\begin{cases} 1 & \text{ if } b\lt b^*\\ -1 & \text{ if } b\ge b^* \end{cases}.\]
Now that we are back to two variables $w$ and $h$, one natural way to think of a model for two variables is to decide on two thresholds (call then $w^*$ and $h^*$ and decide that the model says positive if both the variables are smaller than their thresholds. Mathematically, \[f(w,h)=\begin{cases} 1 & \text{ if } w\lt w^* \text{ and } h\lt h^*\\ -1 & \text{ otherwise } \end{cases}.\]
This seems like a natural generalization to what we had for one variable. So let us plot such a model in two variables (for concreteness let us pick $w^*=350$ and $h^*=150$):

But the above does not look like the linear models we saw before? Where is the line? Indeed this is not a linear model but a decision tree model, which we will see in bit more depth soon.
Let us now come back to the linear models, which we have seen before:

Let us now consider the various desired model class properties for linear models on two variables:
Parsimonious representation
As in the case of one variable, which side of the line gets blue color is one parameter (or more precisely one bit ). So the interesting question is how many parameters do we need to represent the line itself.
Recall that figuring out the number of parameters was easy for linear models in one variable case became trivial once we figured out the mathematical expression for linear models in one variable. It turns out that once we are able to do this for linear models in two variables then figuring out the number of parameters will also become easy for two variables as well.
In case you have not looked at geometry since your school days, worry not! Here is a quick recap on how to mathematically define a line in two dimensions (note that after that we only need to figure out which side is to be colored blue). For the first parameter, figure out where the line "cuts" the vertical axis-- in our case this will be the weight $c$ at which the line cuts the weight axis, like so:

The next parameter is based on how "fast" the line "rises." In our particular case the height grows from $h=0$ to $h=300$. Let us assume that in this change the corresponding weight has changed $300\cdot m$. In other words the $w$ value increases from $w=c$ at $h=0$ to $w=c+300\cdot m$ at $h=300$, like so:

It turn out that it is enough since once we know $c$ and $m$ the line gets fixed. This is because as illustrated here:

Exercise
Convince yourself that the intercept and slope of the line $w=m\cdot h+c$ are indeed $c$ and $m$ as defined above.
After the above, figure out the intercept and slope of all the lines here:

This we can now mathematically define a linear model in two dimensions now: \[\ell(w,h)=\begin{cases} 1 & \text{ if } w \ge m\cdot h+c\\ -1 & \text{ if } w \lt m\cdot h+c\\ \end{cases}.\]
Exercise
Convince yourself that this definition matches the visual description of the linear model we saw above.
Finally, note that we only need three parameters: the values $m$, $c$ and which side of the line defines the blue side. One could ask the same question as we did for the one variable case of whether we need to store all infinitely many value of $m$ and $c$. The answer again is no, but we'll leave that argument as an exercise:
Exercise
Given you are trying to fit a line in a dataset of $n$ points (i.e. a list $(w_1,h_1),\dots,(w_n,h_n)$, how many distinct linear models do we need to consider to be able to guarantee that the line with the best fit lies in that set?
Efficient model training
It turns out that the situation for efficiently training a linear model in two variables is more tricky/complicated than the case in variables. In particular, as we have done so far, let us assume you want to find the optimal linear model for two variables for a dataset that minimizes the number of misclassified data points. While there was a fairly simple/clean algorithm that was provably correct for the one variable case, there is simple algorithm for the two-variable case (in other words, explaining those algorithms is out of scope for this course). However, if you are curious, there exists such an algorithm that can solve the model training problem on dataset with $n$ 2D points in roughly $n^2$ steps (see the 2012 paper by Aronov et al. for more on this, though the specific result I mentioned appeared 1993 paper by Houle ).
Unfortunately, unlike in the one variable case, we cannot improve the runtime of this algorithm to scale linearly in $n$ (doing so would improve the best known runtime for a large number of problems ). By contrast, checking if there is a linear model that has no misclassification can be solved in linear in $n$ number of steps .
A tradeoff?
Note that the above argument gives a tradeoff between overall accuracy and training time: i.e. one can use one variable to have overall smaller accuracy but get a faster model training or one can use two variables to get overall better accuracy with a slower model training.
However, it turns out that in real life there is a way around this tradeoff: see below.
Of course folks use linear models in real life and they are very efficient. So what gives? The idea is that these algorithms do not aim to get the optimal linear model and in fact for datasets that are not perfectly explained by a linear model, there are no known theoretical guarantees on the quality of the approximation that these algorithms achieve. However, these algorithm work pretty well on real-life datasets. We will come back to these algorithms when we study the model training part of the ML pipeline.
Efficient prediction
Like in the one variable case, this basically follows from definition so we leave it as an exercise:
Exercise
Once the linear model $\ell$ (i.e. the intercept $c$, the slope $m$ and which side is the blue color) is fixed, then given a 2D point $(w,h)$ determining its label $\ell(w,h)$ can be done in constant many steps.
Model expressivity
Again as in the case of linear models in one variable, we will not spend much time on this aspect except to point out unless the dataset is really close to explained by a linear model, a linear model will not be able to fit a more complicated dataset (and we have seen examples above where the points were essentially generated from a "non-linear" model). This is why in state-of-the-art ML pipeline, where accuracy is the primary objective, use non-linear models.
Other desirable properties
Like in the case of linear models in one variable, linear models are used in assessing risk of certain health outcomes since it is easier to "explain" the prediction.
Linear model on more than two variables
Finally we consider the most general linear model where we have $d$ input variables. It turns out that the situation for the general $d$ case is very similar to the $d=2$ case. Hence to avoid repeating a bunch of stuff, we will only highlight the desired properties where things differ from the $d=2$ case (properties that are not mentioned hold in essentially same manner as the $d=2$ case).
Parsimonious representation
It turns out that with $d$ input variables, we can specify a line once we fix $d$ parameters and so overall we need $d+1$ parameters (the $+1$ is to specify which side will be blue).
Efficient model training
The references mentioned in the $d=2$ show that the model training on a dataset with $n$ points can be done in roughly $n^d$ steps, which gets worse as $d$ increases. Again, in practice model training aims to only approximate the best possible linear model.
Decision Trees
Before we try we delve into the details on decision trees , we start off with two examples out of which hopefully y'all have seen/heard of at least one about. These examples are related to decision trees (more precisely they are closely related to the prediction step for decision tree models). The first example is of a game show:
Twenty Questions
Twenty questions is where the aim is to guess an unknown term about which a player can ask up to $20$ yes/no questions. Here is a video from one of the episodes from the 1905s show:
(The first three and half minutes which the video above is set up to skip is the introduction of the episode-- it could be a useful anthropological experience.)
The skill in the game comes from the fact that one should ask relevant questions and from an intuitive perspective, at each stage one should ask a question that somehow "gets rid" of "most" of the non-relevant possibilities. Of course in this game there is no restriction on what kind of questions need to be asked (other than it should be a question that has a yes/no answer). However, as we will see later, for decision tree models, we would prefer to restrict the kind of yes/no questions that can be asked.
The next example is a standard computer science algorithm called the binary search :
Binary Search
Binary search solves the following question. Suppose you are given access to $n$ numbers that are listed in increasing order: i.e. $x_0\le x_1\le \cdot \le x_n$ (e.g. the numbers $0,2,3,5,7,8,9$). Now given a number $y$ (e.g. $7$) you want to figure out if there is any index $i$ such that $x_i=y$-- if so, output $1$ else output $-1$ (in the running example, you should output $1$ since we have $x_4=7$).
One can solve the above problem in $n$ steps by just walking through the list and for each value of $i=0,\dots,n-1$ check if $x_i=y$. However one can solve this much more efficiently (in about $\log_2{n}$ steps), like so:
The binary search algorithm only asks the questions of the following form. For any $i=0,\dots,n-1$ is $x_i\le y$ or not. The basic idea behind binary search is to ask this question of the "middle" element because we can always "prune" away half the list.
Exercise
If you have not seen this before, try and convince yourself as to why comparing $y$ with the middle element always gets rid of about half the locations where $y$ could reside.
Hint Recall that $x_0\le x_1\le \cdots x_n$. So if for any index $m$, we have $x_m\le y$-- what can you say whether $x_{m-1}\le y$? What about $x_{m-2}\le y$? What about $x_j\le y$ for any $0\le j\le m$? On the flip side, if $x_m\gt y$-- what can you say about whether $x_{m+1}\gt y$? What about $x_{m+2}\gt y$? What about $x_k\gt y$ for any $k=m,\dots,n-1$? Argue that irrespective of how the comparison $x_m\le y$ pans out, one can always at a minimum rule out indices in $0,\dots,m-1$ OR $m+1,\dots,n-1$ as the potential location for $y$.
It is OK if you do not see why the above algorithm takes $\log_2{n}$ steps if we pick the index $m$ to be the "mid-point" of the interval of indices that have survived at any round. If it helps you feel better, just assume this fast as a given.
What kind of questions can be asked?
We will address this later but at this point, we wanted to note that in 20 Questions, one could basically ask any kind of question while in the binary search the kind of questions that can be asked was restricted (since we could only ask if $x_m\le y$ and not e.g. if $x_m^2+1 \le y^3$.1
When we define decision tree models, we will go with the latter route of more restrictive questions (this makes the model training step potentially easier).
Like in the linear model case, we will start off our discussion with decision trees for one variables. As we will see this model contains the linear model as a special case (and indeed is powerful enough to capture any dataset (though not necessarily in a parsimonious representation.
One variable case
All questions of the form $b\ge b^*?$
To focus our discussion, we will only consider the questions of the form-- $b\ge b^*$? I.e. for the single input variable $b$ we can ask whether is is smaller than a fixed value $b^*$ that we can choose as part of designing the question? Also we will allow the answers to be either $1$ (for the case that $b\ge b^*$), or $-1$ (for the case $b\lt b^*$). For example, the result of the query $b\ge 30$ can be represented in a form that we have seen before:

Decision trees in one variable (informal-ish definition)
A decision tree (model) informally is a set of questions of the form $b\ge b^*$ and the model decides to color a point $b$ blue or yellow based on the answers to the questions that were asked.
Let us consider some examples to make the concept more concrete. The first example is where we just ask the question $b\ge 30$ and if the answer is $1$ then we color $b$ to be blue and yellow otherwise. This leads to the function pictured above, that we have seen before. As if we have not seen multiple representation, we will introduce another one representation for decision tree models. In particular, for the simple decision tree model that we just talked about, here is the corresponding representation:

node in the decision tree. There are two outgoing edges: one labeled $1$ for all values $b$ that satisfy $b\ge 30$ and other labeled with $-1$ for the rest of the values of $b$ (i.e. those that satisfy $b\lt 30$). The final "answer" for the model on the value $b$ is denoted by the leaf nodes, which are presented by squares and are colored blue or yellow.
One can use the decision tree above to do prediction in the natural way. Say we want to see what the above decision tree labels $b=40$. In this case the comparison in the oval evaluates to $1$ so we take the left edge. Then we have reached a leaf that is colored blue, which is what the decision tree will evaluate $40$ to. On the other hand if $b=20$, then the comparison will evaluate to $-1$ and we take the right edge and figure out that $20$ will be colored yellow.
However, as was the case with 20 Questions or binary search we can ask more than one question. E.g. here is another decision tree that asks three questions in total:

root (i.e. the top-most) node and depending on what the comparison answer is you take the left or the right edge. Then you the comparison in the child node and repeat the procedure again. This time you will end up in a leaf node and you have the predicted color at that stage.
Exercise
Convince yourself that the above decision tree predicts $b=5$, $b=15$, $b=75$ and $b=200$ to be of color blue, yellow, blue and yellow respectively.
Further, convince yourself that if one were to represent the color that the above decision tree gives to the $b$ values on the number line, then you will get the following:

Class of decision trees in one variable (formal-ish definition)
A decision tree is formally defined as a labeled binary tree (i.e. you have nodes, other than leaf nodes, with two outgoing labels-- one labeled as $1$ and the other as $-1$ and each leaf is colored blue or yellow. Note that a leaf node has no outgoing edge). Further each node other than the leaf nodes (also called internal nodes) have a comparison of the form $b\ge b^*$ associated with them).
The class of decision tree models is the collection of all possible decision trees in one variable. Note that this is indeed an infinite class like the class of linear models but as we will see shortly, this class is way more expressive.
You call this a tree?
If you have not studied the notion of trees in computer science , our current notion of tree seems odd:

E.g. here are two questions: why is the root at the top? What are the leaves at the bottom? I do not have a good answer other than to shrug and say that we computer scientists got it upside down :-)
Properties of decision tree model in one variable
For reasons that will become clear shortly, we will consider the desired properties in a slightly different order. In particular, we will start with the expressivity of this model class first:
Model expressivity
We first being with an exercise that shows that linear models in one variable is a special case of decision trees in one variable:
Exercise
Argue that any linear model in one variable $b$ can be represented as some decision tree on variable $b$.
Hint: If you are lost on how to argue the above, perhaps the following two equivalent formulations of the first decision tree we saw in this section will help:


So the above show that the class of decision tree models is at least as expressive as the class of linear models (both of course one one variable). However, it turns out that the class of decision tree models are strictly more powerful than the class of linear models:
Exercise
Argue that there is a decision tree model in one variable $b$ that cannot be represented as any linear model on variable $b$.
Hint: If you are lost on how to argue the above, perhaps the second decision tree we saw in this section will help. For completeness, we again present the two equivalent representations:


Finally, we argue that the class of decision tree models can capture all possible datasets of $n$ data points:
Exercise
Argue that any dataset with $n$ points (i.e. it has input variable value $b_i$ and a corresponding label $y_i$ (which is $1$ or $-1$)) for $i=1,\dots,n$, then there exists a decision tree with about $n$ internal nodes ($n-1$ if you want to be precise) that can perfectly classify the dataset.
Hint: Think of how you would solve the problem for $n=2$ (if it helps, we would point out that this also works for a linear model but not for larger $n$) by using one one question. Now try to extend the result to $n=3$. If you can do that try to do it for $n=4$. (Note that your arguments should work no matter where the points $b_1,]dots,b_4$ can be any four points and the corresponding labels $y_1,\dots,y_4$ can be any of the $2^4=16$ possibilities (each $y_i$ has two choices and each of the four choices can be made independently leading to $2\times 2\times 2\times 2=2^4$ possibilities). By now you should be able to spot a pattern-- use that pattern to solve this problem for arbitrary $n\gt 4$.
Parsimonious representation
We start off with how many parameters we need to represent a decision tree to represent a dataset with $n$ entries. From the last exercise we know that we need to first have a tree on at most $n-1$ internal nodes. Then we need to figure out the threshold value for comparison for each $n-1$ internal node as well as the colors of the at most $n$ leaf nodes.2. Thus, once we fix the binary tree, we will need up to $2n$ parameters. One can also argue that one needs of the order of $n$ parameters to represent such a tree. In case you are curious about a more mathematically precise, you can get the lowdown here (the notion of binary search tree is essentially our notion of decision tree but with the notion of $-1$ and $1$ on the edges of our decision trees being switched):
Irrespective of the exact number of parameters needed to represent a decision tree it is at least $n$ and grows with the size of the dataset. On the other hand the number of parameters needed to represent a linear model in one variable is fixed. Just to be sure, you are not dozing off:
Exercise
Why would a decision tree model need number of parameters that grows with the dataset size while we only need two parameters for linear model? In particular, how would you reconcile this discrepancy?
Thus, we are in a situation that if we want to be able to represent any possible dataset, then we will need as many parameters as using the dataset itself as the model. Thus, to get a parsimonious class of decision tree model, we have to consider suitable subsets of decision trees. For example, one my only consider decision tree with at most $m$ internal nodes, where $m$ is a parameter for the entire class. Typically, we would like to have $m\ll n$.
Efficient model training
For simplicity for exposition, we consider the case of $m\le n-1$: i.e. we have the power to exactly represent any dataset with $n$ points. The goal then if the following. Given a dataset on $n$ points (i.e. $n$ pairs $(b_1,y_1),\dots,(b_n,y_n)$) compute a decision tree with the smallest number of internal nodes that exactly represent the $n$ points.
For simplicity, let us assume that $b_1\lt b_2\lt \cdots b_n$.
Let us start with the simplest case: i.e. there is only one "transition" point in the labels. In other words, looking at the points in increasing values of $b_i$, we have that the first so many points are labeled red (or green) and the rest are labeled green (red respectively), like so:

Exercise
Can you think of a decision tree that can perfectly classify the above dataset with one internal node? Further can you compute it in around $n$ steps?
You basically fit it using a linear model in this case:

Regarding efficiency, note that all we need to do if compute the location of $i$ but this can be done doing a linear scan of the numbers from $b_n$ to $b_1$, which takes $n$ steps (and each step needs some constant amounts of check).
Let us wok with the next simplest case: i.e. there are two "transition" points in the labels from $b_j\to b_{j+1}$ and $b_i\to b_{i+1}$, like so:

Exercise
Can you think of a decision tree that can perfectly classify the above dataset with two internal nodes? Further can you compute it in around $n$ steps?
You basically fit it using two comparisons that handle each "monochromatic" sequence of points from the "right":

Regarding efficiency, note that all we need to do if compute the locations of $i$ and $j$ but this can be done doing a linear scan of the numbers from $b_n$ to $b_1$, which takes $n$ steps (and each step needs some constant amounts of check).
In particular, carrying on the argument along these lines, one can actually solve the general problem:
Exercise
In about $n$ steps, compute an optimal decision tree in one variable that perfectly fits an arbitrary dataset with $n$ labeled points.
Hint: Do a linear scan from $b_n$ to $b_1$ and create a comparison for each transition in the labels during this scan. If you would rather not, you can drop the ask of proving that this is indeed the decision tree with fewest comparison/questions.
Efficient prediction
As with the linear model, the prediction algorithm naturally follows from the definition of the decision tree. In particular, given a value $b$, start with the root see if doing the comparison with value $b$ gives an answer of $1$ or $-1$ and based on the answer the correspondingly labeled edge. If you reach a leaf node, then you just output the color of the leaf otherwise you repeat the whole procedure you did at the root.
Consider for example, the following decision tree:

When we do prediction on $b=150$ and $b=70$ on the decision tree above, we trace the red and green path respectively and deduce that they are colored yellow and blue respectively:

We now consider the efficiency of doing prediction on a decision tree. Convince yourself that
Exercise
The number of steps needed to compute the decision tree models prediction on $b$ is the number of comparisons made in the algorithm above. In particular, this is the same as the number of edges needed to go from the root node to the relevant leaf node.
The number of edges needed to go from the root node to a given leaf node is known as the depth of the leaf node in the decision tree. Thus, the worst case number of steps needed to do a prediction for a decision tree is the maximum depth of a leaf node-- this quantity is also known as the depth of the decision tree.
Thus, in the training phase, we would like to learn a decision tree that explains the given dataset with the minimum depth. This gets a bit complicated by the fact that the same dataset can have decision trees of different depth that perfectly fit it. For example, consider the following dataset with $n=4$ points:

The algorithm for training that we alluded to earlier would result in the following decision tree:

Note that the decision tree above has depth $3$. However, one can do better:
Exercise
Show that the dataset above with four points can also be perfectly fit with a decision tree on $3$ internal nodes and depth of $2$.
Hint: Look above!
However, it turns out that one can
Exercise
Modify the algorithm from the exercise in the training section to output an optimal decision tree that in addition also minimizes its depth.
Hint: Take inspiration from binary search and start off with a comparison for the "middle transition point" and continue.
Other desirable properties?
It turns out that decision trees, like linear model, decision tree models are explainable as well. This is because for a given $b$ value one can state the outcomes of the relevant comparisons. In many situations, these comparisons can be easily mapped to some real life measurements that say a patient can understand, which improves the explainability. We note that a necessary condition is that one has to list a small number of comparisons: otherwise in general listing as many comparisons as the size of the dataset is not a viable option.
Decision tree models on two variables
Class of decision trees in two variables (formal-ish definition)
Actually, the definition is follows by a simple modification to the definition for the one variables case: now instead of comparing the value of just one variable now each internal node can do a comparison on either of the two variables (for the moment assume that we can only compare either $w$ or $h$ but not together).
For example, consider the following decision tree in variables $w$ and $h$:

Indeed we saw this decision tree earlier but in the following representation:

Decision tree models on two or more variables
Like in the two-variable case, a decision tree on more than two variable allows comparisons in each internal node to compare any of the $d$ input variables. Next, we walk through the desired properties of class of ML models, in the same order we did in the one variable case. Doing a detailed exposition on each property is outside the scope of this course-- instead we will briefly go through each property of general decision trees.
Model expressivity
As in the one variable case, we argue that the class of decision tree models can capture all possible datasets of $n$ data points with $d$ input variables:
Exercise
Argue that any dataset with $n$ points (with $d$ input variables) there exists a decision tree with about $n\cdot d$ internal nodes that can perfectly classify the dataset.
Hint: One can "isolate" any "corner" point in the dataset with $d$ comparisons-- one comparison for each input variable. Once that is done, the rest of the points can be handles iteratively. The algorithms runtime may scale like $n^d$.
Parsimonious representation
As in the one variable case, the whole class of decision tree models cannot be represented with few parameters (since it can represent any dataset). Thus, if we want parsimonious representation, we will need to consider a sub-class of decision trees: e.g. we could restrict the number of internal nodes and/or its depth.
Efficient model training
Unlike one variable case, the situation is much more complex. In many situations, computing the "optimal" decision tree is computationally hard. On the other hands, many heuristics have been proposed that compute approximately optimal decision tree from the given dataset. See the survey by Murthy for more technical details.
Efficient prediction
As in the one variable case, the efficiency of this step depends on the depth of the corresponding decision tree.
Other desirable properties?
As in the one variable case, decision trees (assuming they are not too deep or big) seem amenable to being explainable.
Neural Networks
Unlike our exposition of linear models and decision tree model, we will not consider neural networks on one input variable. Most of our discussion will be for the case of two variables (where as before it is easier to draw pictures). Further, we will not go into as much technical depth as we did for linear and decision tree models since the underlying math is bit more involved.3
Simplification galore!
Much more so than the other two models, we will be simplifying the treatment of neural networks. In particular, we will be presenting a very strict sub-class of neural networks. Later on, we will briefly mention the generalization needed to do deep learning , which is a fancy re-branding of ML techniques that have existed for decades and folks are already wondering if deep learning is over-hyped . But that is a story for another time.
The main high level idea
Recall that in a linear model on two variables we divided up the 2D space of allowable points into a blue part and a yellow part using a line. At a super-high level, the idea in neural networks is to first transform the set of allowable points, like so:


Where we we get our hands on these transforms?
Acknowledgments
All of the animations on this page is from this page on linear algebra using python by Raibatak Das .
One common class of transform is the class of linear transforms (which are related to linear model but are not the same). These are easy to define if one is familiar with linear algebra but since we do not assume linear algebra knowledge, we will give some examples of some linear transforms:
- The first transform is that of
rotation, which literally rotates the set of allowed points (the transform above is a rotation):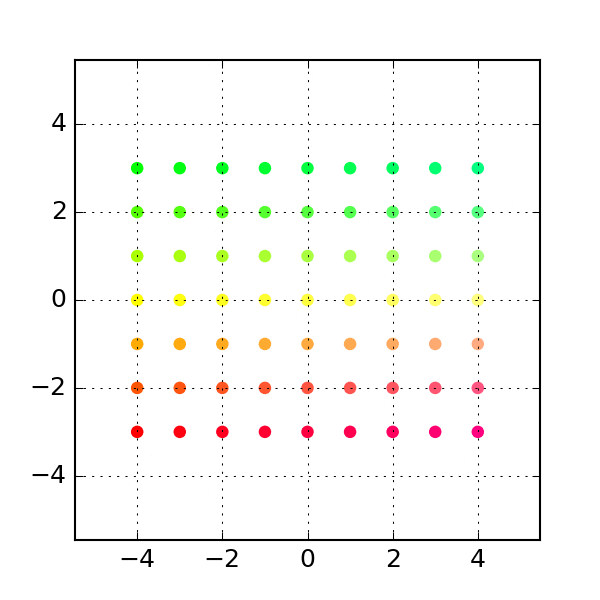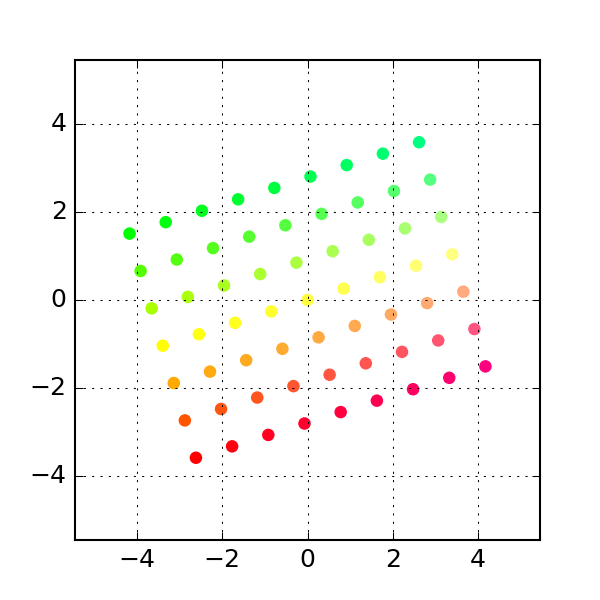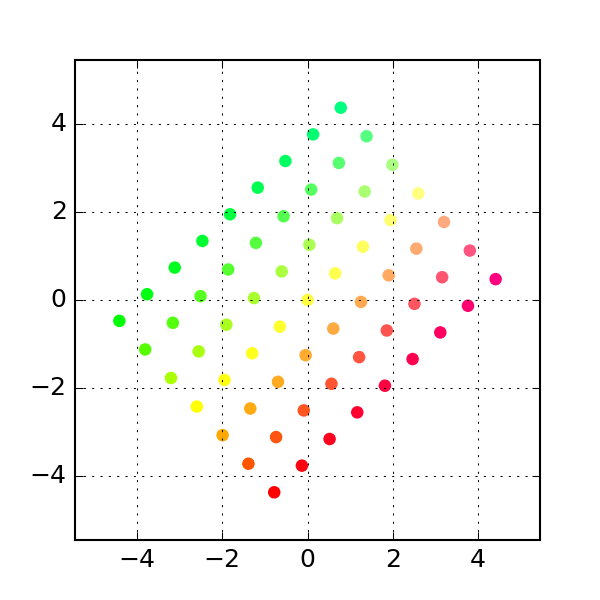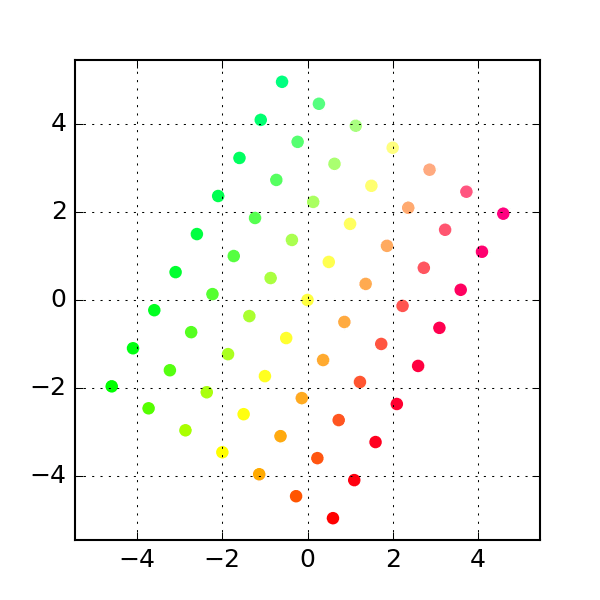
- The second transform is that of
shear:
- The third transform is that of
permutation:
- Finally, we present a more general
linear transform: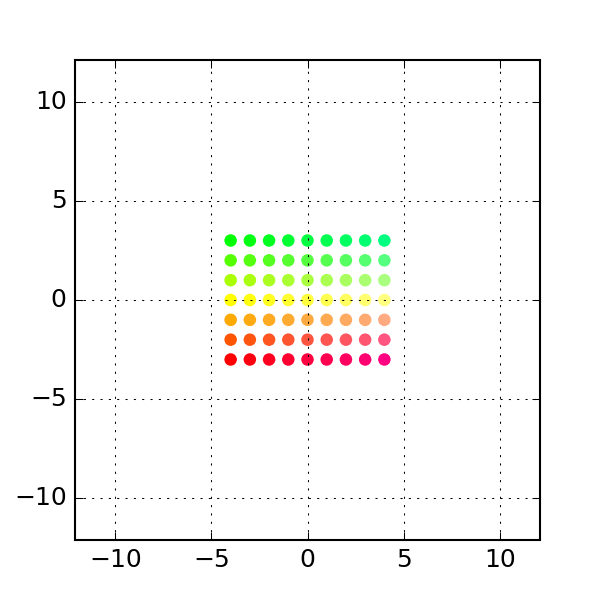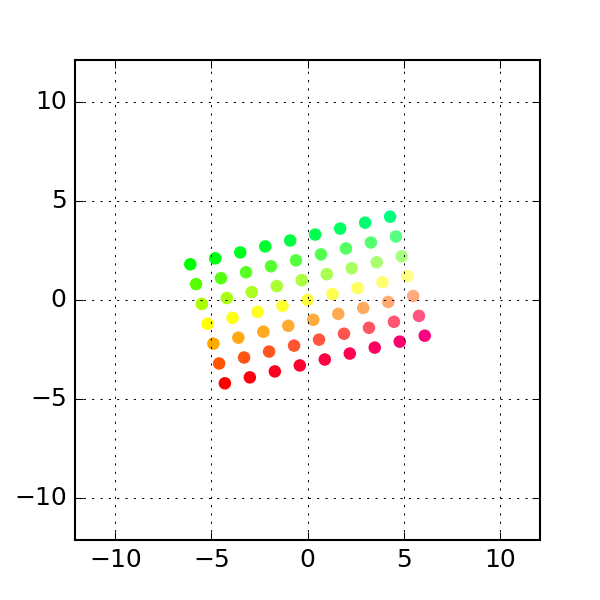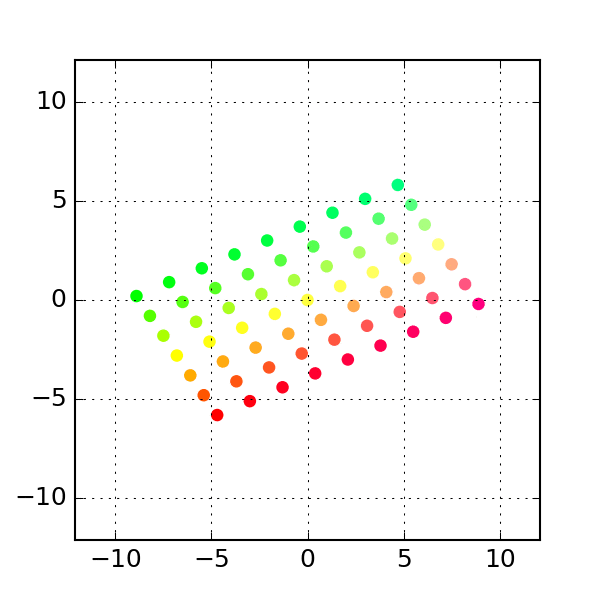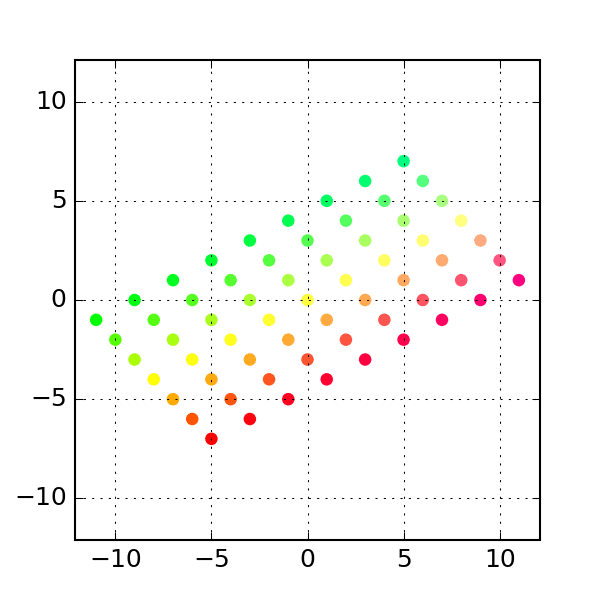
Going beyond linear transforms
So it turns out that using a linear transform followed by using a linear model does not buy us much (or anything):
Exercise
Argue that a linear transform followed by a linear model is equivalent to (another) linear model in the original space.
Hint: Can you "reverse" the whole process?
Click here to see an outline of the answer
It turns out that there is always a inverse map for a linear map (assuming the original linear map is non-trivial in a precise mathematical sense), like so:

Using this inverse transform on the linear model gives the linear model in the original space:

The power of neural networks comes from the fact that it uses non-linear transform (and then applies a linear model as before):
Rectified linear unit (ReLU)
Simply put, ReLU just zeroes out any negative value. In our 2D-example the ReLU function is applied to both the $w$ and $h$ values.
For example, let us consider the following linear transform that both rotates and translates the set of points:



One natural question to as is if we gained something by adding the ReLU function at the end? Answering this question in its full generality is hard, so we should ask a weaker question: Do we at least get a different model than a linear model? In particular, is the model any different from the following linear model?

It turns out that neural networks are indeed different from linear models (in two variables)!4
What we gained from using ReLU
Let us focus on the points that are the linear transform ended up having negative weight, which we truncated to $0$. Note that after applying ReLU, many points get mapped to the same point. For example the points (after the linear transformation) $(-10,150)$ and $(-20,150)$ will both get mapped to the point $(0,150)$ after applying RELU. In other words all points $(-w,h)$ for any $w\gt 0$ get mapped to $(0,h)$. For example, all point on the red line in the figure below get mapped to $(0,150)$:

What the above means is that there are many original weight and height pairs that get mapped to height axis and get assigned the same color, like so (denoted by the darker blue and yellow lines):

If we "unroll" the application of RELU, here is how the original set of points get colored:

By inspection, we can argue that the model is not a linear model!
Exercise (Neural networks in one variable)
We now briefly give a strong reason for why we did not consider neural networks in one variable-- it turns out that this class of models is exactly the same as the class of linear models in one variable. In this exercise, you will argue this claim.
First we more precisely define neural networks in one variable. First a linear transform in one variable is a map $b \mapsto m\cdot b +c$. So if $\ell$ is the final linear model that we will apply after applying ReLU to the linear transform of $b$, then we get the following description of a neural networks in one variable: \[NN(b) := \ell\left(ReLU\left(m\cdot b+c\right)\right).\]
Argue that for any linear model $\ell$, the model $NN$ is also a linear model.
What is so deep about this?
Nothing actually :-) Less glibly, what we have seen so far is a single layer neural network, where the single layer refers to the fact that we have only applied the linear map + ReLU combo only once. In current applications of neural networks, we apply this combination of linear transform+ReLU multiple times before we apply the final linear model at the end. It turns out that one can represent these applications of these layers of linear transform+ReLU top-down and then the "deep" refers to the there being multiple layers one after the other. See e.g. this figure by Adir Deshpande's blog post on neural network architectures shows the GoogLeNet
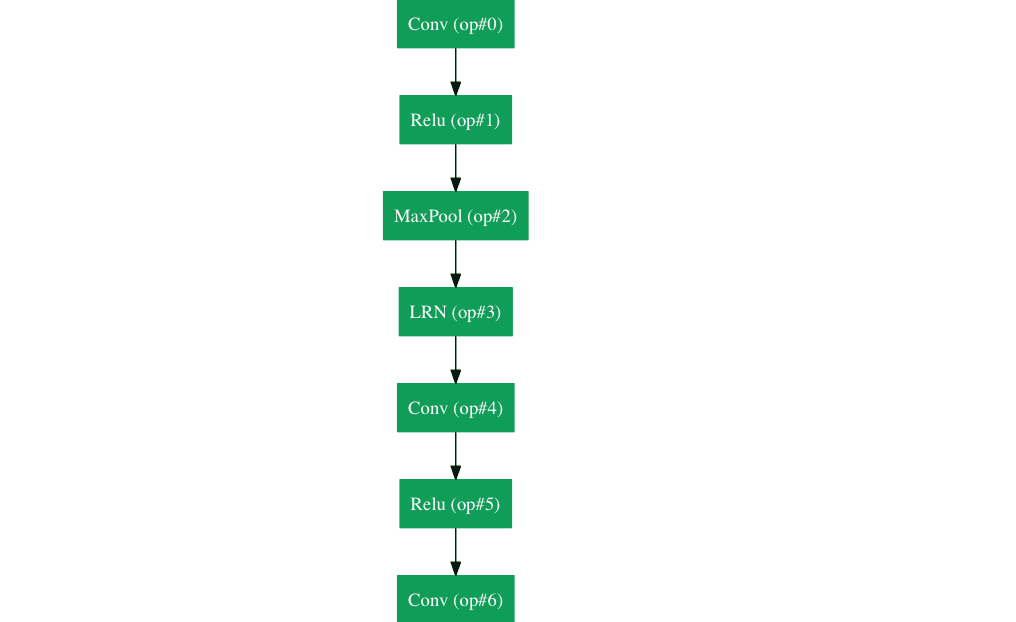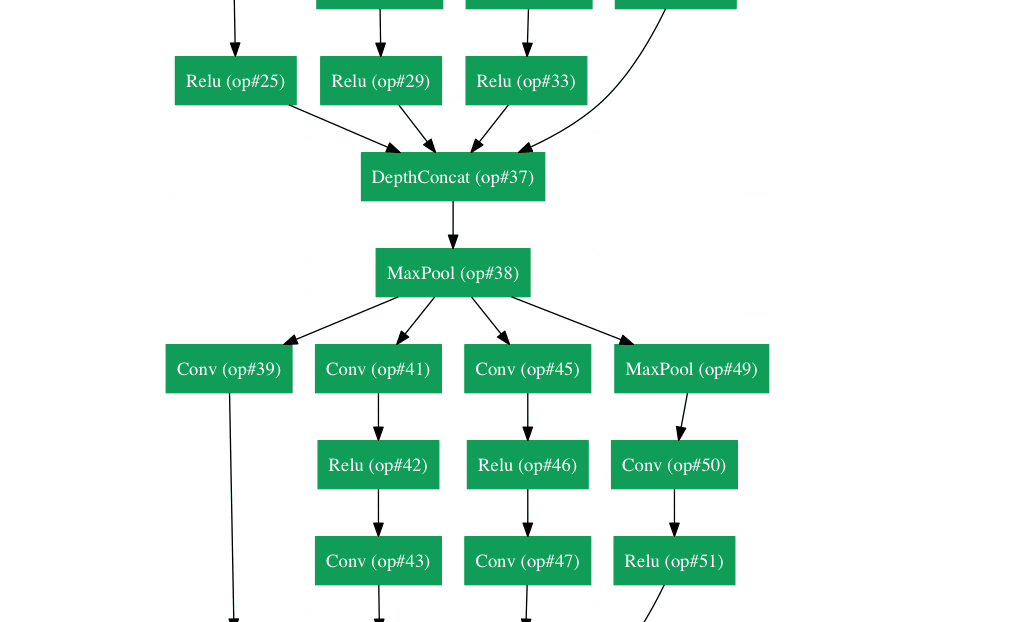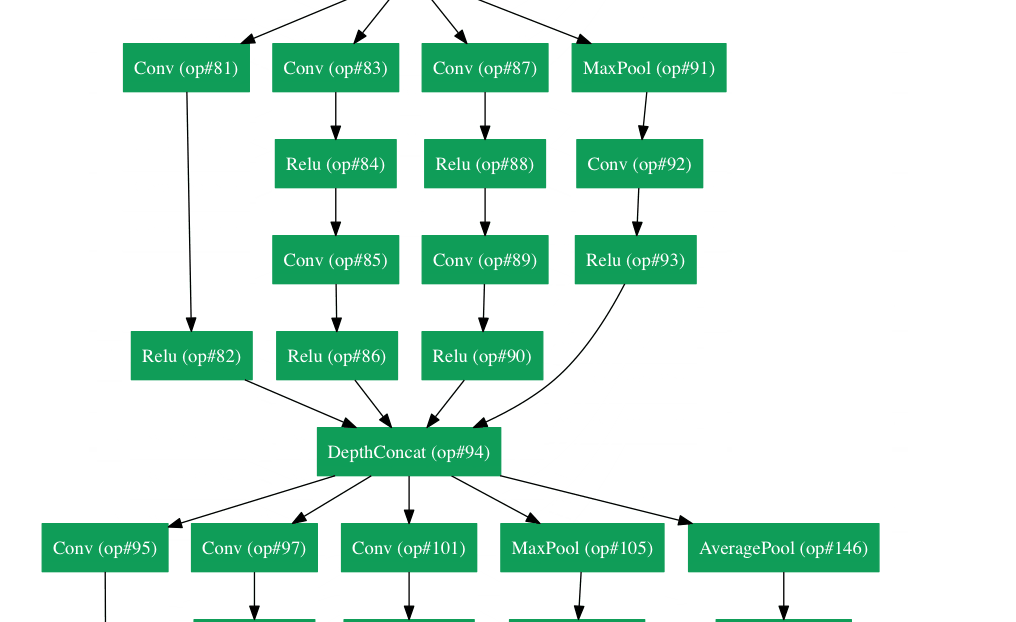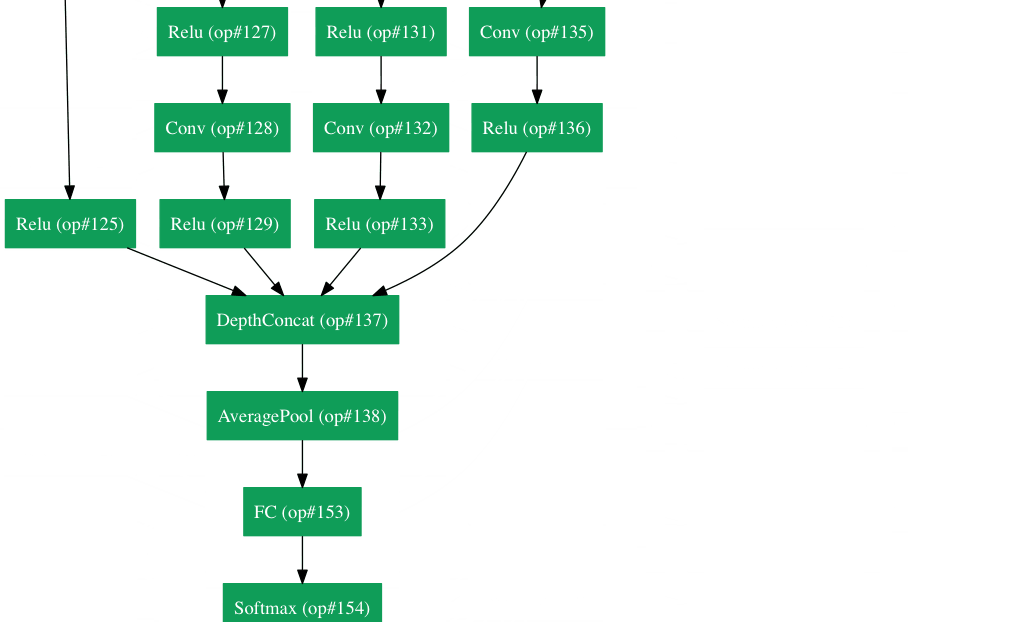
Other transforms exist
First it turns out that one can pick other non-linear functions other than ReLU. Second, combining these possibilities with the large number of linear transforms implies that one can have many kinds of layers one can put in a neural network is quite large.
While it is a perfectly valid question to ask on how many layers we should pick (and what kind of transform each layer should be), answering these questions is out of the scope of this course.
Desired properties of neural networks
Model expressivity
It is known that neural networks can approximate any functions and hence can represent any labeled dataset exactly. Covering this result is out of the scope of this course.
Parsimonious representation
It turns out that neural networks (at least the recent ones with multiple layers) actually are not parsimonious. In fact, these models are overparameterized. Given this, it is somewhat surprising that in many widely used applications neural networks do not seem to overfit . Covering this result is out of the scope of this course.
Efficient model training
Not much is known theoretically on the efficiency of model training for neural networks. In practice, algorithms such as (stochastic) gradient descent work well in practice but its theoretical properties are not well understand in the context of training neural networks. We will very briefly come back to gradient descent when we consider the model training steps of the ML pipeline.
Efficient prediction
The efficiency prediction depends on the how many layers are used in the neural network as well as the efficiency of computing each layer. Covering this out of the scope of the course.
Other desirable properties?
Neural networks are notorious for not being explainable. We will return to this topic later in the course.
A digression: A Jupyter notebook exercise
Before we move on, let's use Jupyter notebook to get a sense for how which model class you pick can affect your accuracy at the end:
Load the notebook
Log on to Google Colab . Then download the ML pipeline notebook from the notebooks page (here is a direct link). Load the notebook into Google Colab , which would look like this:

Ignore most of the notebook
The default instruction still applies: make sure you run all the cells in sequence.
The notebook trains ML models on the COMPAS dataset but you can ignore most of the notebook safely for now. Pay attention to two things:
- At the very bottom of the notebook states the accuracy of the linear model (where we are by default training on a random $80\%$ subset of the dataset and the accuracy is measured on a random $20\%$ random sample as the testing dataset):

- look for the "cell" titled
Choose the model class. This is the cell that looks like this:
Play around with choosing among the three model classes as well as removing/adding various input variables/column names and see how the accuracy changes at the bottom of the notebook.
Next Up
We will finish going through the rest of the steps in the ML pipeline.